Lecture 05
Jump to navigation
Jump to search
(Previous lecture) ... (Next lecture)
Homology - I: the Principles
- What you should take home from this part of the course
- Understand what homology means and what can be deduced from the fact that two sequences are homologues.
- Understand that the similarity of amino acids' biological functions depends on the amino acid but also on the context.
- Know that sequence similarity can be measured, based on amino acid pair scores.
- Be familiar with the concept of a scoring matrix and with scoring matrices in common use for sequence alignment; appreciate the differences between these matrices and the models embodied in them.
- Be familiar with the principle of a dotplot and tools to generate a dotplot.
- Links summary
- The Dotlet applet on the Web.
- Exercises
- Read Walter Fitch's review (pdf) (2000, Trends Genet 16:227-231) on the topic of homology and familiarize yourself with the concepts!
- Read Sean Eddy's summary of the theory behind and the development of the BLOSUM62 matrix.
Lecture Slides
Slide 001
Lecture 05, Slide 001
It is commonplace today that far-reaching conclusions about biological function are drawn from the inference of homology between proteins or protein domains.
It is commonplace today that far-reaching conclusions about biological function are drawn from the inference of homology between proteins or protein domains.
The concept of homology
Slide 002
Lecture 05, Slide 002
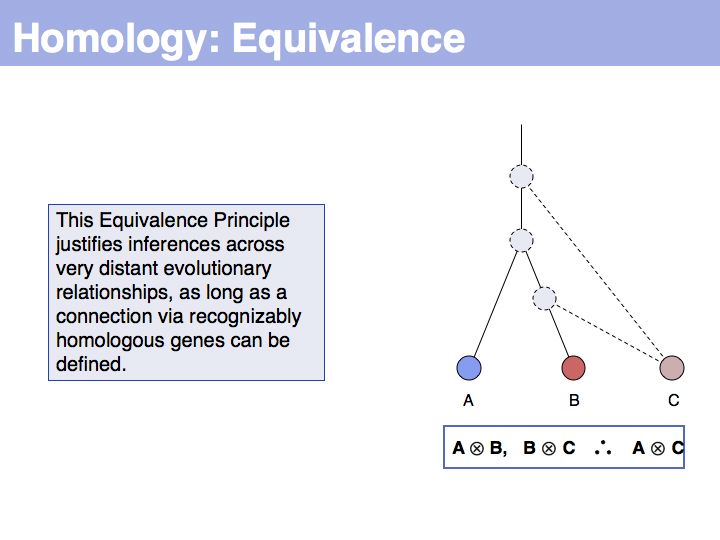
The concept of homologous sequences is extensively applied wherever genes or organisms are compared. It is especially important for the study of biology through Model organisms, where inferences about one species are made from data gathered in another. These inferences are justified, because (and to the degree that) the species are related ...
The concept of homologous sequences is extensively applied wherever genes or organisms are compared. It is especially important for the study of biology through Model organisms, where inferences about one species are made from data gathered in another. These inferences are justified, because (and to the degree that) the species are related ...
Slide 003
Lecture 05, Slide 003
The word Homology has a precise meaning (in biology) and should not be used differently! Read Walter Fitch's excellent review (2000, Trends Genet 16:227-231) on the topic.
We conjecture that paralogous genes have similar but importantly different functions because otherwise one of the copies would be superfluous ,and would be lost under evolutionary drift. Note that we are especially interested in orthologous relationships, because we infer that two orthologues would have maintained the "same" functions. However please note that when one or both organisms have undergone additional duplications after speciation, multiple orthologues may exist. Fitch has proposed the term isoorthologues for that pair of genes with the "same" function among a family. While this is an excellent proposal that would address much confusion, unfortunately the term has not caught on. Thus, rather than rely on a shared understanding of expansive vocabulary in the community, define your concepts explicitly and adhere to your definitions.
The word Homology has a precise meaning (in biology) and should not be used differently! Read Walter Fitch's excellent review (2000, Trends Genet 16:227-231) on the topic.
We conjecture that paralogous genes have similar but importantly different functions because otherwise one of the copies would be superfluous ,and would be lost under evolutionary drift. Note that we are especially interested in orthologous relationships, because we infer that two orthologues would have maintained the "same" functions. However please note that when one or both organisms have undergone additional duplications after speciation, multiple orthologues may exist. Fitch has proposed the term isoorthologues for that pair of genes with the "same" function among a family. While this is an excellent proposal that would address much confusion, unfortunately the term has not caught on. Thus, rather than rely on a shared understanding of expansive vocabulary in the community, define your concepts explicitly and adhere to your definitions.
Slide 004
Lecture 05, Slide 004
Slide 005
Lecture 05, Slide 005
The equivalence principle might not be obvious. Given that the cenancestral sequences (the last common ancestor sequences) of the pairs {A,B} and {B,C} are different, how do those relationships tell us something about the relationship between {A,C}?
The equivalence principle might not be obvious. Given that the cenancestral sequences (the last common ancestor sequences) of the pairs {A,B} and {B,C} are different, how do those relationships tell us something about the relationship between {A,C}?
Slide 006
Lecture 05, Slide 006
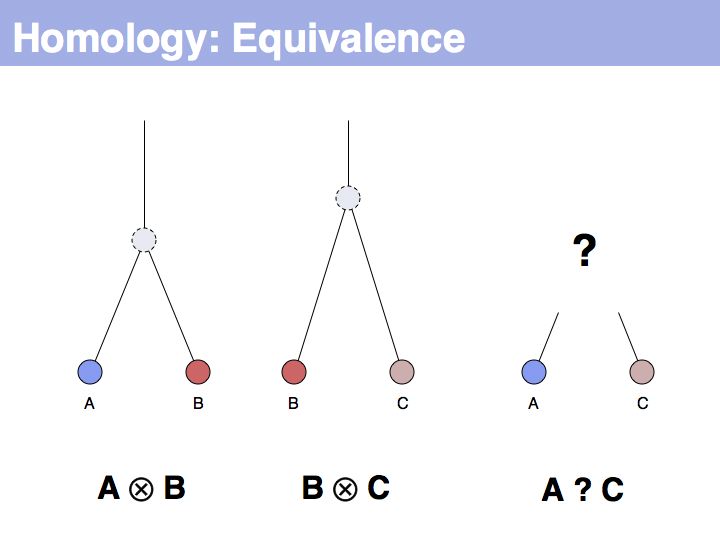
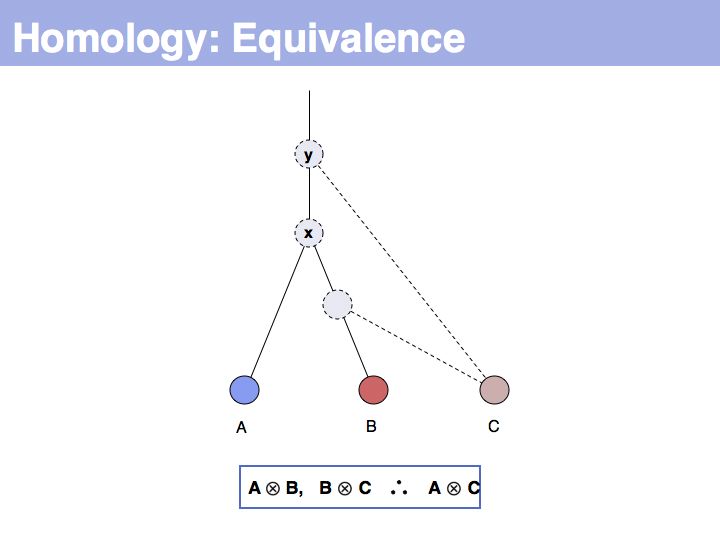
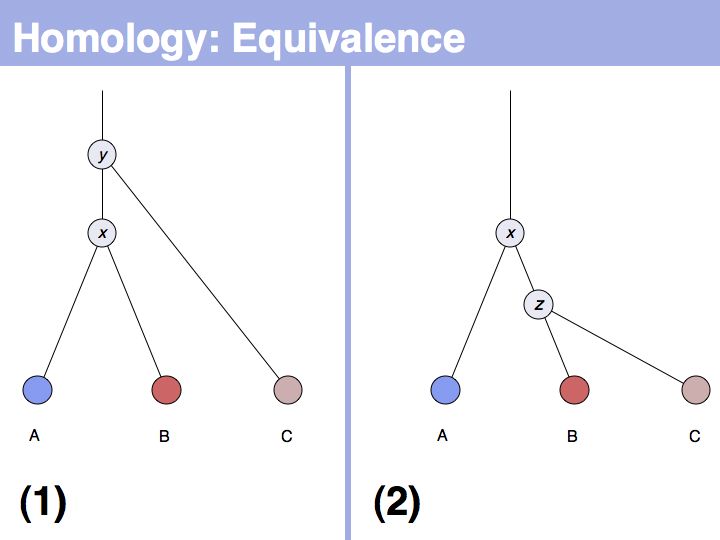
The answer is based on the fact that there are two, but only two, possibilities for the relationship between {A,B} and {B,C}, drawn above (assuming a simple, dichotomous branching relation between the genes). (1): the divergence between {B,C} happened before {A,B}, at node y. (2): the divergence between {B,C} happened after {A,B}, at node z. Thus we do not know which of the cases is the correct one, the ancestral gene for all three genes can be either x or y ...
The answer is based on the fact that there are two, but only two, possibilities for the relationship between {A,B} and {B,C}, drawn above (assuming a simple, dichotomous branching relation between the genes). (1): the divergence between {B,C} happened before {A,B}, at node y. (2): the divergence between {B,C} happened after {A,B}, at node z. Thus we do not know which of the cases is the correct one, the ancestral gene for all three genes can be either x or y ...
Slide 007
Lecture 05, Slide 007
... but we do know that some common ancestral gene exists for all three sequences, and therefore they must all three be homologous.
... but we do know that some common ancestral gene exists for all three sequences, and therefore they must all three be homologous.
Slide 008
Lecture 05, Slide 008
Slide 009
Lecture 05, Slide 009
Slide 010
Lecture 05, Slide 010
Inferring homology
Slide 011
Lecture 05, Slide 011
Many obviously homologous genes have very low sequence identity. In this example, the aligned sequences of green- and red- fluorescent protein share 57 of 239 identical residues, i.e. the sequence identity is 23.8%.
Many obviously homologous genes have very low sequence identity. In this example, the aligned sequences of green- and red- fluorescent protein share 57 of 239 identical residues, i.e. the sequence identity is 23.8%.
Slide 012
Lecture 05, Slide 012
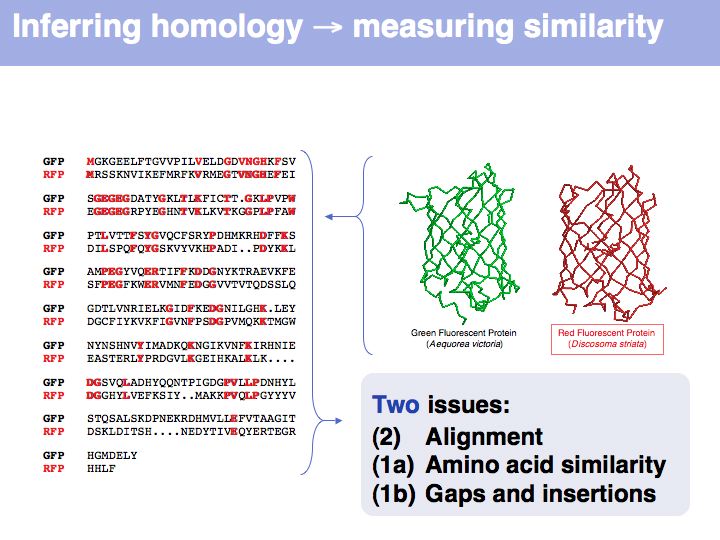
Obviously, the fraction of identical residues depends on the alignment and we need to consider how the right alignment can be obtained. But even before we can start aligning, we need to define a metric between amino acids, to quantify amino acid similarity because the right alignment should give us good similarity, not just a large percentage of identical residues. So the second issue comes before the first issue. And there is an additional second issue: how do we treat sequence insertions resp. deletions in the alignment?
Obviously, the fraction of identical residues depends on the alignment and we need to consider how the right alignment can be obtained. But even before we can start aligning, we need to define a metric between amino acids, to quantify amino acid similarity because the right alignment should give us good similarity, not just a large percentage of identical residues. So the second issue comes before the first issue. And there is an additional second issue: how do we treat sequence insertions resp. deletions in the alignment?
Slide 013
Lecture 05, Slide 013
Measuring amino acid similarity
Slide 014
Lecture 05, Slide 014
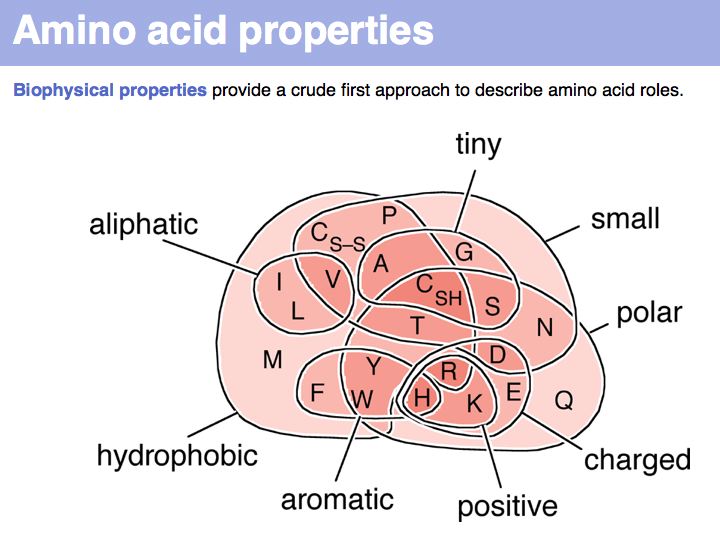
Biophysical amino acid properties can be used to group amino acids into sets. Each memebr of this set could be considered to be similar, according to that property. Alternatively, biophysical properties can be tabulated and similarity computed according to a scale. Such numerical scales may include properties as *the free energy of transfer from water to octanol;
*the pKa of the sidechain;
*the volume;
*the accessible surface area (ASA), and many more.
For more details, see the Wikipedia article on the standard amino acids.
Biophysical amino acid properties can be used to group amino acids into sets. Each memebr of this set could be considered to be similar, according to that property. Alternatively, biophysical properties can be tabulated and similarity computed according to a scale. Such numerical scales may include properties as *the free energy of transfer from water to octanol;
*the pKa of the sidechain;
*the volume;
*the accessible surface area (ASA), and many more.
For more details, see the Wikipedia article on the standard amino acids.
Slide 015
Lecture 05, Slide 015
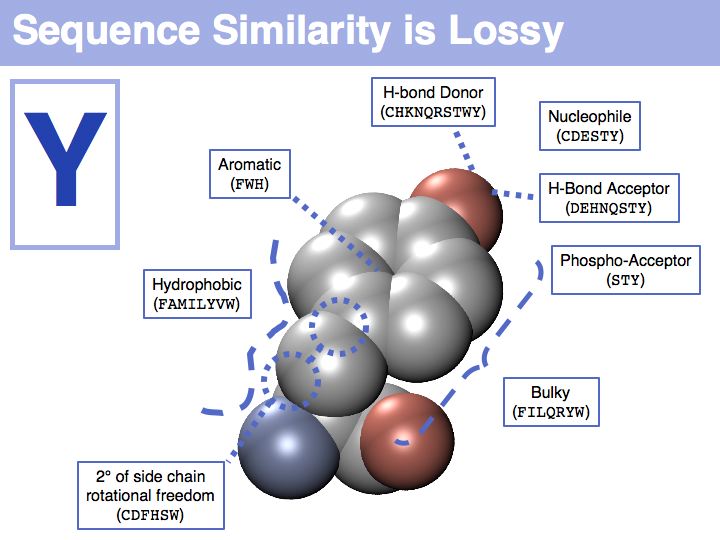
In a sequence, all information about the molecular properties of an amino acid is condensed into into the single letter code (or other labels for "abstractions" of amino acids). However, how similar one amino acid is to other amino acids depends on the role it plays for the structure and/or function of a protein. Depending on this role, an amino acid like tyrosine would be considered e.g. similar to other hydrophobic amino acids, or other side chains that can accept H-bonds. However these two groups are non-overlapping sets!
In a sequence, all information about the molecular properties of an amino acid is condensed into into the single letter code (or other labels for "abstractions" of amino acids). However, how similar one amino acid is to other amino acids depends on the role it plays for the structure and/or function of a protein. Depending on this role, an amino acid like tyrosine would be considered e.g. similar to other hydrophobic amino acids, or other side chains that can accept H-bonds. However these two groups are non-overlapping sets!
Slide 016
Lecture 05, Slide 016
Slide 017
Lecture 05, Slide 017
Scoring matrices
Slide 018
Lecture 05, Slide 018
A scoring matrix is a computational tool that associates each pair of residues with a number. In this example, the score of the pair {E,D} from an alignment is read out from a scoring matrix.
A scoring matrix is a computational tool that associates each pair of residues with a number. In this example, the score of the pair {E,D} from an alignment is read out from a scoring matrix.
Slide 019
Lecture 05, Slide 019
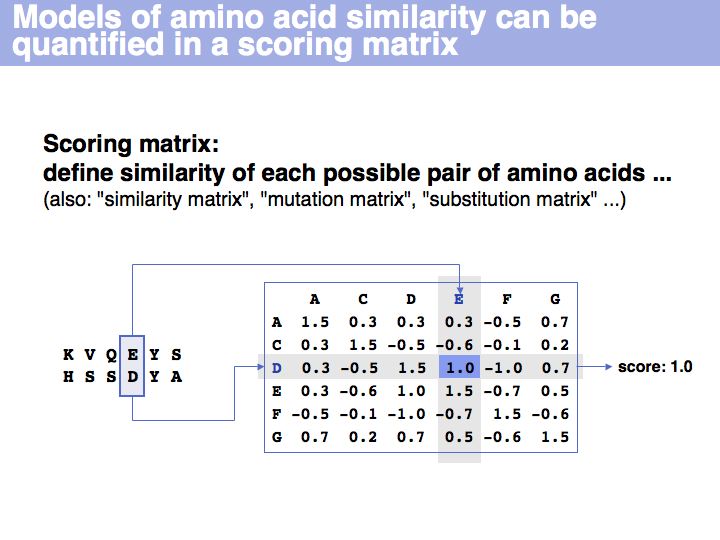
The Identity Matrix is valid only at small evolutionary distances (where all similarity matrices give comparable results). Currently, it is primarily used for nucleotide sequence comparisons, where the concept of similarity does not really apply. But the more realistic the model of the evolutionary process is, the less information is discarded. Better models make less assumptions. Many interesting biological relationships have been uncovered precisely because we have been able to perform very sensitive homology searches.
The Identity Matrix is valid only at small evolutionary distances (where all similarity matrices give comparable results). Currently, it is primarily used for nucleotide sequence comparisons, where the concept of similarity does not really apply. But the more realistic the model of the evolutionary process is, the less information is discarded. Better models make less assumptions. Many interesting biological relationships have been uncovered precisely because we have been able to perform very sensitive homology searches.
Slide 020
Lecture 05, Slide 020
There is more to this matrix than might seem apparent. Mechanistically speaking, similar codons arise from single nucleotide changes. But functionally speaking, the genetic code minimizes the biophysical effect of mutations! Thus similar codons code for "similar" amino acids.
There is more to this matrix than might seem apparent. Mechanistically speaking, similar codons arise from single nucleotide changes. But functionally speaking, the genetic code minimizes the biophysical effect of mutations! Thus similar codons code for "similar" amino acids.
Slide 021
Lecture 05, Slide 021
The model that M.O. Dayhoff proposed in 1978 departs from an ab initio attempt to define amino acid similarity to an empirical approach.
The model that M.O. Dayhoff proposed in 1978 departs from an ab initio attempt to define amino acid similarity to an empirical approach.
Slide 022
Lecture 05, Slide 022
Slide 023
Lecture 05, Slide 023
The matrix above is not the Dayhoff matrix, it is just called "MDM". It was derived from the original 1978 Dayhoff matrix for PAM250 by rescaling it to give a constant score for identities (1.5). This may save computational resources but is an unfounded, arbitrary change. Nevertheless, this matrix was the one that was in most common use for many years.
The matrix above is not the Dayhoff matrix, it is just called "MDM". It was derived from the original 1978 Dayhoff matrix for PAM250 by rescaling it to give a constant score for identities (1.5). This may save computational resources but is an unfounded, arbitrary change. Nevertheless, this matrix was the one that was in most common use for many years.
Slide 024
Lecture 05, Slide 024
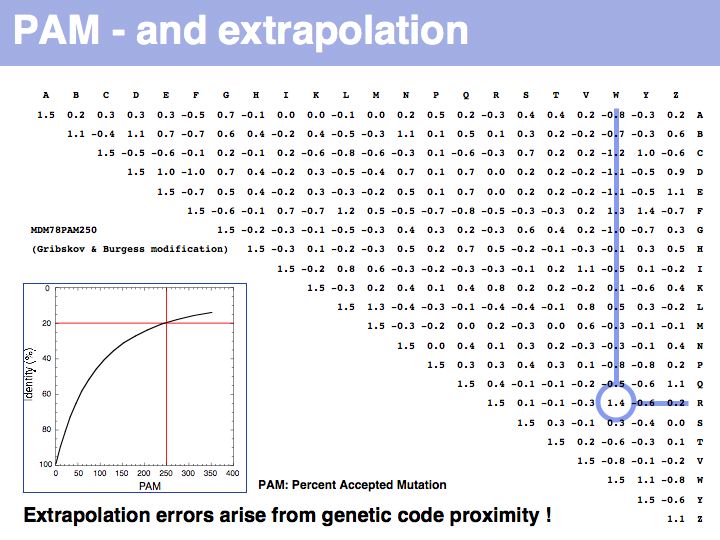
Two of arginine's six codons (CGG and AGG) can be changed to the tryptophan codon TGG by a single point mutation. Thus these two amino acids, which have quite different biophysical properties and distributions, are defined as almost as similar as a pair of identitcal amino acids by this matrix that was constructed by extrapolation from highly related sequences. The source data that M.O. Dayhoff had used was biased towards sequences in which secondary, functional selection may not have had time to occur after an initial mutation event. Accordingly, this process of extrapolation is expected to inappropriately favour exchanges that can be coded by a single nucleotide substitution. Thus, while the model is rigorous and well designed, the source data limits its accuracy.
The inset picture shows the relationship between PAM - percent accepted mutation and % residue identity. This is not a linear relationship, due to back-mutation. In the limit of infinitely many accepted mutations, sequence identity should still be around 5% and not 0.
Two of arginine's six codons (CGG and AGG) can be changed to the tryptophan codon TGG by a single point mutation. Thus these two amino acids, which have quite different biophysical properties and distributions, are defined as almost as similar as a pair of identitcal amino acids by this matrix that was constructed by extrapolation from highly related sequences. The source data that M.O. Dayhoff had used was biased towards sequences in which secondary, functional selection may not have had time to occur after an initial mutation event. Accordingly, this process of extrapolation is expected to inappropriately favour exchanges that can be coded by a single nucleotide substitution. Thus, while the model is rigorous and well designed, the source data limits its accuracy.
The inset picture shows the relationship between PAM - percent accepted mutation and % residue identity. This is not a linear relationship, due to back-mutation. In the limit of infinitely many accepted mutations, sequence identity should still be around 5% and not 0.
Slide 025
Lecture 05, Slide 025
Slide 026
Lecture 05, Slide 026
Read Sean Eddy's excellent summary of the theory behind and the development of the BLOSUM62 matrix.
Read Sean Eddy's excellent summary of the theory behind and the development of the BLOSUM62 matrix.
Slide 027
Lecture 05, Slide 027
Slide 028
(deleted)
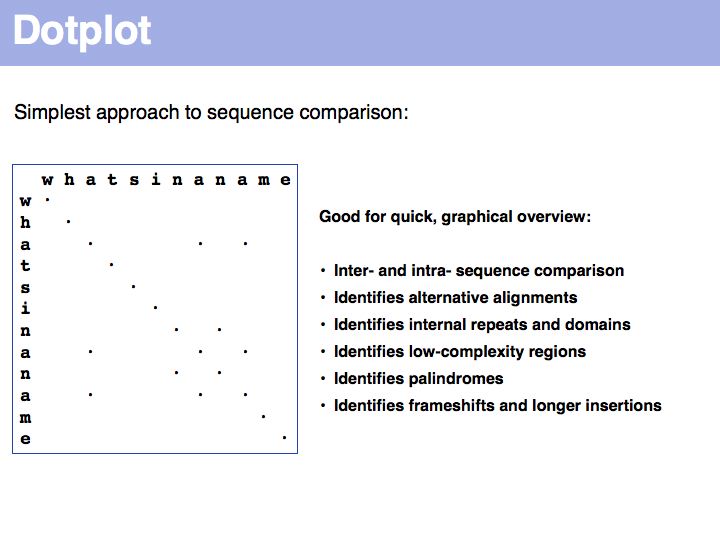
Sequence comparison: Dotplots
Slide 029
Lecture 05, Slide 029
For examples of biological sequence features in a dotplot: see [http://www.isrec.isb-sib.ch/java/dotlet/dotlet_examples.html here].
For examples of biological sequence features in a dotplot: see [http://www.isrec.isb-sib.ch/java/dotlet/dotlet_examples.html here].
Slide 030
Lecture 05, Slide 030
The [http://www.isrec.isb-sib.ch/java/dotlet/Dotlet.html Dotlet applet] on the Web. A of standalone tool for local installation is Dotter, also available on the Web as JDotter.
The [http://www.isrec.isb-sib.ch/java/dotlet/Dotlet.html Dotlet applet] on the Web. A of standalone tool for local installation is Dotter, also available on the Web as JDotter.
