Difference between revisions of "Lecture 10"
Jump to navigation
Jump to search



| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="padding: 5px; background: #FF4560; border:solid 2px #000000;"> | + | |
| + | |||
| + | <!-- div style="padding: 5px; background: #FF4560; border:solid 2px #000000;"> | ||
'''Update Warning!''' | '''Update Warning!''' | ||
| − | This page has not been revised yet for the | + | This page has not been revised yet for the 2008 Fall term. |
| − | </div> | + | Some of the slides will probably be reused, but please consider the page as a whole out of date |
| + | as long as this warning appears here. Also, the lectures may be taught in a different sequence. | ||
| + | </div --> | ||
| + | | ||
| | ||
| + | <small>[[Lecture_09|(Previous lecture)]] ... [[Lecture_11|(Next lecture)]]</small> | ||
| + | |||
| − | + | <div class="toclimit-3">__TOC__</div> | |
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| + | <br> | ||
| + | <div style="padding: 2px; background: #879BFA; border:solid 1px #AAAAAA;"> | ||
| + | ==Interpreting Protein Structure== | ||
| + | </div><br> | ||
| + | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | <br> |
| + | <div style="padding: 10 px; background: #B0B8D7; border:solid 1px #AAAAAA;"> | ||
| + | ====Objectives for this part of the course==== | ||
| + | </div><br> | ||
| + | * Understand that PDB files contain coordinate information, measured in an orthogonal coordinate system in Å (0.1 nm, 10<sup>-10</sup>m ).<br> | ||
| + | * Have a sense of the approximate sizes of biological objects.<br> | ||
| + | * Be familiar with the most frequently recurring conformations in protein structure.<br> | ||
| + | * Be aware that these recurring units are just labels and there is some degree of arbitrariness involved in assigning them to real coordinates.<br> | ||
| + | * Understand that more frequently observed conformations are more favourable - for function, for stability or both.<br> | ||
| + | * Be able to superimpose two structures and compare their differences.<br> | ||
| + | * Be able to find structures that are similar to a query.<br> | ||
| − | ===== | + | <br> |
| − | [[ | + | <div style="padding: 10 px; background: #B0B8D7; border:solid 1px #AAAAAA;"> |
| + | ====Links summary==== | ||
| + | </div><br> | ||
| + | *[http://dunbrack.fccc.edu/bbdep/ Backbone Dependent Rotamer Library]<br> | ||
| + | *[http://www.biochem.ucl.ac.uk/bsm/atlas/ Atlas of Hydrogen Bonds]<br> | ||
| + | *[http://en.wikipedia.org/wiki/Protein_structural_alignment Structural Alignment (Wikipedia)]<br> | ||
| + | *[http://www.ncbi.nlm.nih.gov/Structure/VAST/vast.shtml '''VAST''' at the NCBI]<br> | ||
| + | *[http://ekhidna.biocenter.helsinki.fi/dali/start '''DALI '''fold classification in Helsinki]<br> | ||
| + | *[http://www-cryst.bioc.cam.ac.uk/~homstrad/ '''HOMSTRAD''' at the University of Cambridge]<br> | ||
| + | *[http://en.wikipedia.org/wiki/Structural_alignment_software List of '''Structural Alignment Software''' (Wikipedia)]<br> | ||
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| − | ===== | + | <div style="padding: 10 px; background: #879BFA; border:solid 1px #AAAAAA;"> |
| − | + | ==Lecture slides== | |
| + | </div><br> | ||
| + | <br> | ||
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| − | ==== | + | <br> |
| − | + | <br> | |
| + | <div style="padding: 10 px; background: #B0B8D7; border:solid 1px #AAAAAA;"> | ||
| + | ===Analysis of coordinate geometry=== | ||
| + | </div><br> | ||
| + | <br> | ||
| − | |||
======Slide 006====== | ======Slide 006====== | ||
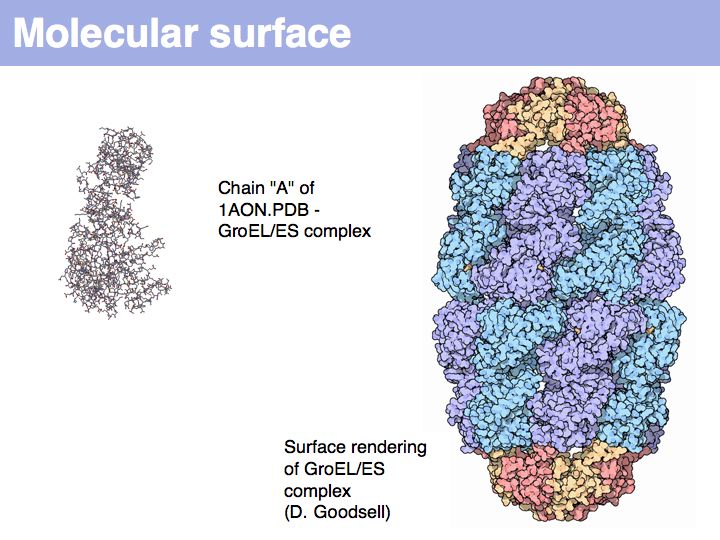
| − | [[Image: | + | [[Image:10_slide006.jpg|frame|none|Lecture 10, Slide 006<br> |
| − | + | It is useful to view structures as a spatially integrated map of annotations. Spatial relationships provide the context that allows mechnistic, molecular interpretations to observed functions and behaviour. | |
]] | ]] | ||
======Slide 007====== | ======Slide 007====== | ||
| − | [[Image: | + | [[Image:10_slide007.jpg|frame|none|Lecture 10, Slide 007<br> |
]] | ]] | ||
======Slide 008====== | ======Slide 008====== | ||
| − | [[Image: | + | [[Image:10_slide008.jpg|frame|none|Lecture 10, Slide 008<br> |
| − | + | In this example: calculate the distance between the phenolic oxygen and a backbone carbonyl in a protein structure. | |
]] | ]] | ||
======Slide 009====== | ======Slide 009====== | ||
| − | [[Image: | + | [[Image:10_slide009.jpg|frame|none|Lecture 10, Slide 009<br> |
]] | ]] | ||
======Slide 010====== | ======Slide 010====== | ||
| − | [[Image: | + | [[Image:10_slide010.jpg|frame|none|Lecture 10, Slide 010<br> |
]] | ]] | ||
======Slide 011====== | ======Slide 011====== | ||
| − | [[Image: | + | [[Image:10_slide011.jpg|frame|none|Lecture 10, Slide 011<br> |
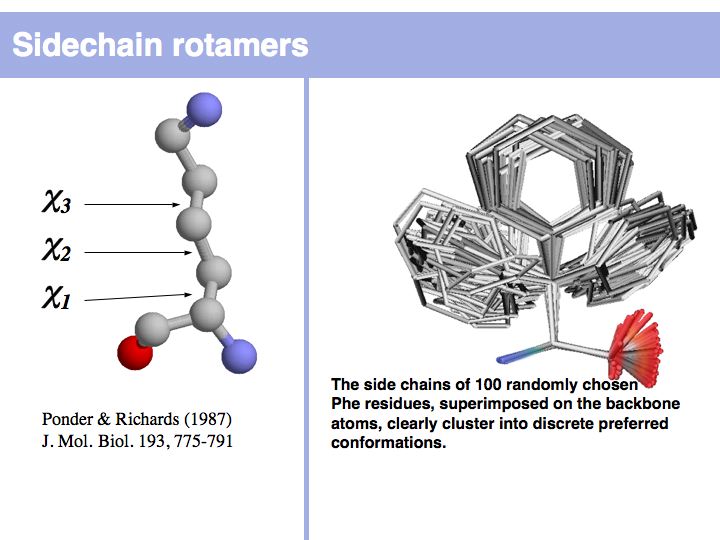
| − | + | Rotamers are low-energy conformations of side-chain dihedral angles. Only a small number of rotamer states and combinations are significantly populated in natural proteins. This tremendously simplifies protein structure modelling and prediction problems. However it also guides analysis, e.g. in enzyme active sites the rotamers often exist in strained, rare conformations. See the [http://dunbrack.fccc.edu/bbdep/ Backbone Dependent Rotamer Library], compiled by Roland Dunbrack. | |
]] | ]] | ||
======Slide 012====== | ======Slide 012====== | ||
| − | [[Image: | + | [[Image:10_slide012.jpg|frame|none|Lecture 10, Slide 012<br> |
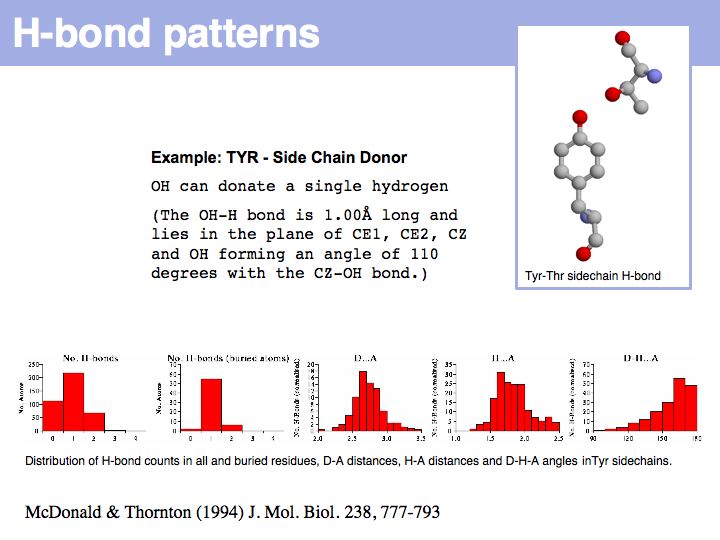
| − | + | Hydrogen bonds have clear and well defined conformational preferences. The ideal donor-acceptor distance is betwen 2.7 and at most 3.5 Å, the angles between the non-hydrogen donor and acceptor atoms vary only to a small degree. One can view them as mechanisms to "lock-in" parts of protein structure. Cf. the [http://www.biochem.ucl.ac.uk/bsm/atlas/ Atlas of Hydrogen Bonds] compiled by Ian McDonald and Janet Thornton. | |
| − | |||
| − | |||
| − | [ | ||
| − | |||
| − | ] | ||
| − | |||
| − | |||
| − | |||
]] | ]] | ||
======Slide 015====== | ======Slide 015====== | ||
| − | + | <small>omitted</small> | |
| − | |||
======Slide 016====== | ======Slide 016====== | ||
| − | [[Image: | + | [[Image:10_slide016.jpg|frame|none|Lecture 10, Slide 016<br> |
| − | + | A set of coordinate ''points'' has no surface! Ascribing a surface to coordinates, in order to map coordinate sets to physical molecules, requires to consider the volume of space that is '''occupied''' by atoms, i.e. space, cannot be invaded by other molecules. | |
]] | ]] | ||
======Slide 017====== | ======Slide 017====== | ||
| − | [[Image: | + | [[Image:10_slide017.jpg|frame|none|Lecture 10, Slide 017<br> |
]] | ]] | ||
======Slide 018====== | ======Slide 018====== | ||
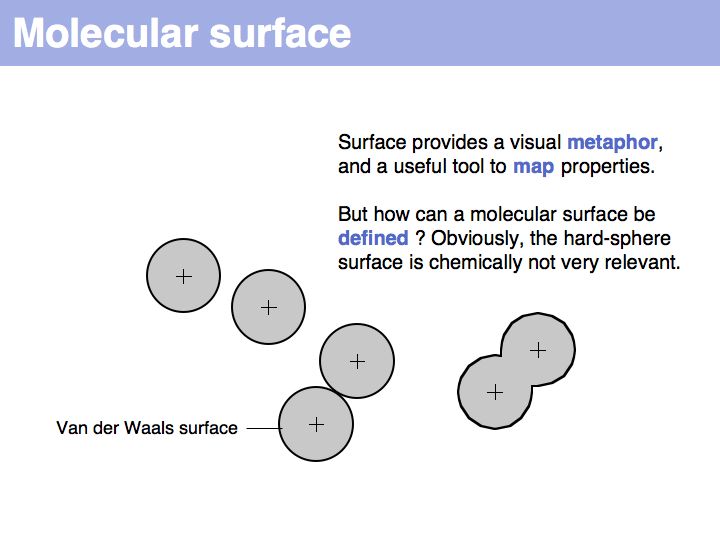
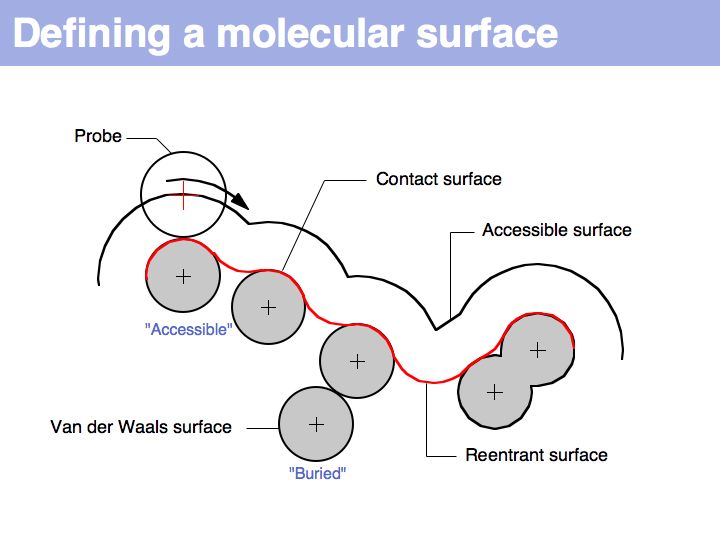
| − | [[Image: | + | [[Image:10_slide018.jpg|frame|none|Lecture 10, Slide 018<br> |
| − | + | A molecular surface can be defined as the boundary that excludes a probe. Commonly, a probe of 1.4 Å radius is used - this is the spehrical approximation of a water molecule and thus this probe defiens a '''solvent accessible surface'''. | |
]] | ]] | ||
======Slide 019====== | ======Slide 019====== | ||
| − | [[Image: | + | [[Image:10_slide019.jpg|frame|none|Lecture 10, Slide 019<br> |
| − | + | The "Accessible Surface" depends on the probe radius. | |
]] | ]] | ||
======Slide 020====== | ======Slide 020====== | ||
| − | [[Image: | + | [[Image:10_slide020.jpg|frame|none|Lecture 10, Slide 020<br> |
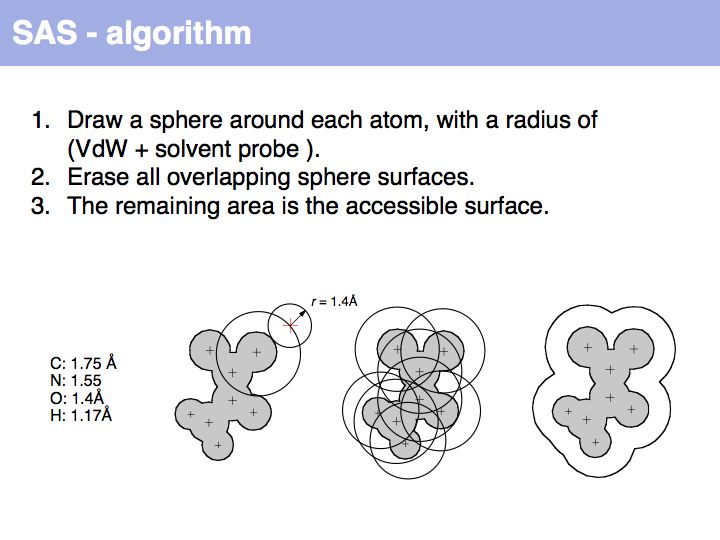
| + | An easy way to calculate SAS (solvent accessible surface) areas is to (1) randomly place a given number of points on a sphere around an atom center, (2) erase points that are overlapped by neighboring atoms' spheres and (3) count the number of points that remain. The fraction of remaining points times the surface area of the original sphere approximates the solvent accessible surface area. Surface areas of individual residues are often expressed as relative values, i.e. the actual accessible surface area of a sidechain divided by the area of a maximally solvent-exposed sidechain. This characterizes the degree to which a sidechain is buried or accessible in a protein structure. | ||
| + | ]] | ||
| + | ======Slide 022====== | ||
| + | [[Image:10_slide022.jpg|frame|none|Lecture 10, Slide 022<br> | ||
| + | Surfaces represent the parts of a protein that interact with the surroundings. In this example, the electrostatic potential mapping shows how an electrostatic potential gradient attracts the substrate molecule into Acetylcholine-esterase's active site. | ||
| + | ]] | ||
| + | |||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <div style="padding: 10 px; background: #B0B8D7; border:solid 1px #AAAAAA;"> | ||
| + | ===Structure contains recurring units=== | ||
| + | </div><br> | ||
| + | <br> | ||
| + | ======Slide 024====== | ||
| + | [[Image:10_slide024.jpg|frame|none|Lecture 10, Slide 024<br> | ||
| + | From the earliest protein structures, it was recognized that many of the local conformations of structure recur within and between proteins. | ||
]] | ]] | ||
| − | ======Slide | + | ======Slide 031====== |
| − | [[Image: | + | [[Image:10_slide031.jpg|frame|none|Lecture 10, Slide 031<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 032====== |
| − | [[Image: | + | [[Image:10_slide032.jpg|frame|none|Lecture 10, Slide 032<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 033====== |
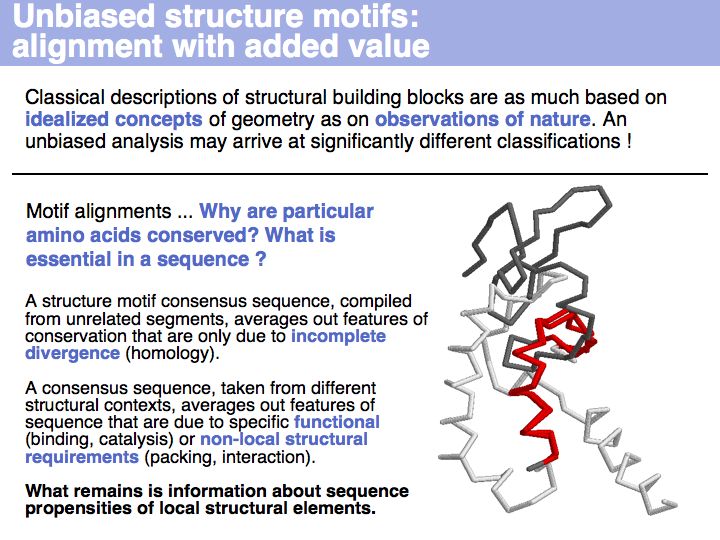
| − | [[Image: | + | [[Image:10_slide033.jpg|frame|none|Lecture 10, Slide 033<br> |
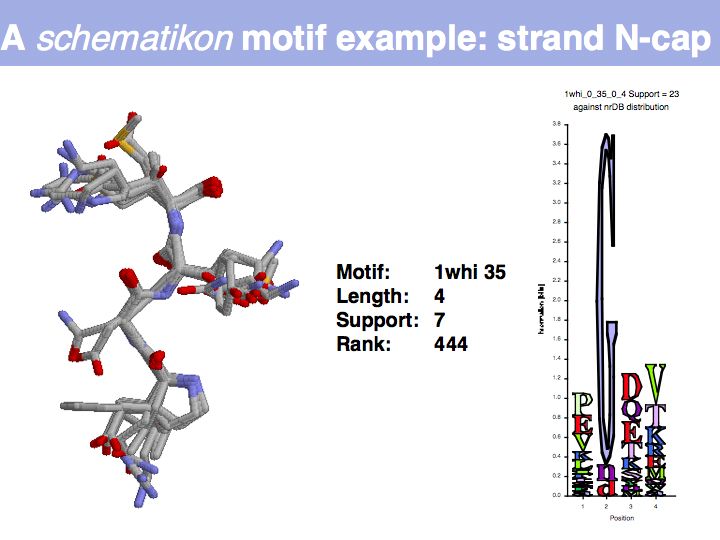
| + | Motifs represent (presumably) low-energy patterns of conformations. They can be discovered in structure datasets by looking for patterns that recur more frequently than expected by random chance. In almost all cases, they have significant statistical propensities to favour particular amino acids in particular positions. This is an example from the schematikon dictionary of recurring structural motifs. he motif is a peptide of length four, recurring seven times. I is ranked in position 444 of all statistiacaly significant motifs. the overlap of backbone atoms is shown in the structural superposition, the propensity for individual amino acids is shown in the sequence logo. Note that the source data consists of non-hmologous protein structures, i.e. the sequence propensities do not represent '''conservation''' (since they are not related by common ancestry, but they represent examples of '''convergent evolution'''. | ||
| + | ]] | ||
| + | ======Slide 034====== | ||
| + | [[Image:10_slide034.jpg|frame|none|Lecture 10, Slide 034<br> | ||
]] | ]] | ||
| − | ======Slide | + | ======Slide 035====== |
| − | [[Image: | + | [[Image:10_slide035.jpg|frame|none|Lecture 10, Slide 035<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 036====== |
| − | [[Image: | + | [[Image:10_slide036.jpg|frame|none|Lecture 10, Slide 036<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 037====== |
| − | [[Image: | + | [[Image:10_slide037.jpg|frame|none|Lecture 10, Slide 037<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 038====== |
| − | [[Image: | + | [[Image:10_slide038.jpg|frame|none|Lecture 10, Slide 038<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 039====== |
| − | [[Image: | + | [[Image:10_slide039.jpg|frame|none|Lecture 10, Slide 039<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 040====== |
| − | [[Image: | + | [[Image:10_slide040.jpg|frame|none|Lecture 10, Slide 040<br> |
]] | ]] | ||
| − | ======Slide | + | ======Slide 041====== |
| − | [[Image: | + | [[Image:10_slide041.jpg|frame|none|Lecture 10, Slide 041<br> |
]] | ]] | ||
| − | |||
| − | |||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <div style="padding: 10 px; background: #B0B8D7; border:solid 1px #AAAAAA;"> | ||
| + | ===Propensity predicts stability=== | ||
| + | </div><br> | ||
| + | <br> | ||
| + | |||
| + | ======Slide 043====== | ||
| + | [[Image:10_slide043.jpg|frame|none|Lecture 10, Slide 043<br> | ||
| + | Mean field approach - context is constant: averaged context is an approximation to a constant context. | ||
| + | What does Boltzmann-like distribution mean: there is a relationship between frequency of observed microstate | ||
]] | ]] | ||
| − | ======Slide | + | ======Slide 044====== |
| − | [[Image: | + | [[Image:10_slide044.jpg|frame|none|Lecture 10, Slide 044<br> |
]] | ]] | ||
| − | |||
| − | |||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <div style="padding: 10 px; background: #B0B8D7; border:solid 1px #AAAAAA;"> | ||
| + | ===Methods: RMSD and superposition=== | ||
| + | </div><br> | ||
| + | <br> | ||
| + | |||
| + | ======Slide 046====== | ||
| + | [[Image:10_slide046.jpg|frame|none|Lecture 10, Slide 046<br> | ||
| + | RMSD or root mean square deviation is simply the square root of the average sum of squared coordinate distances. However, this is just a measure of the relationship between two sets of points in space - it depends on the disynace between the point sets, their rotation and the quantitatiy we are interested in: their intrinsic structural similarity. See also: [http://en.wikipedia.org/wiki/Protein_structural_alignment Structural Alignment (Wikipedia)] | ||
]] | ]] | ||
| − | ======Slide | + | ======Slide 047====== |
| − | [[Image: | + | [[Image:10_slide047.jpg|frame|none|Lecture 10, Slide 047<br> |
| + | A meaningful comparison of structural segments requires that the coordinate sets at first be optimally '''superimposed''': this means find a translation and rotation that minimizes the remaining RMSD. | ||
| + | ]] | ||
| + | ======Slide 048====== | ||
| + | [[Image:10_slide048.jpg|frame|none|Lecture 10, Slide 048<br> | ||
| + | Several pre-superimposed structure sets are available on the Web: [http://www.ncbi.nlm.nih.gov/Structure/VAST/vast.shtml '''VAST''' at the NCBI] [http://ekhidna.biocenter.helsinki.fi/dali/start '''DALI '''fold classification in Helsinki], [http://www-cryst.bioc.cam.ac.uk/~homstrad/ '''HOMSTRAD''' at the University of Cambridge]. | ||
| + | ]] | ||
| + | ======Slide 049====== | ||
| + | [[Image:10_slide049.jpg|frame|none|Lecture 10, Slide 049<br> | ||
| + | [http://en.wikipedia.org/wiki/Structural_alignment_software List of '''Structural Alignment Software''' (Wikipedia)] | ||
| + | ]] | ||
| + | ======Slide 050====== | ||
| + | [[Image:10_slide050.jpg|frame|none|Lecture 10, Slide 050<br> | ||
]] | ]] | ||
| − | ======Slide | + | ======Slide 052====== |
| − | [[Image: | + | [[Image:10_slide052.jpg|frame|none|Lecture 10, Slide 052<br> |
]] | ]] | ||
| − | ======Slide | + | |
| − | [[Image: | + | |
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <div style="padding: 10 px; background: #B0B8D7; border:solid 1px #AAAAAA;"> | ||
| + | ===Structural knowledge - mechanistic explanations=== | ||
| + | </div><br> | ||
| + | <br> | ||
| + | |||
| + | ======Slide 068====== | ||
| + | [[Image:10_slide068.jpg|frame|none|Lecture 10, Slide 068<br> | ||
]] | ]] | ||
| − | |||
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | ]] | + | <br> |
| + | <br> | ||
| + | ---- | ||
| + | <small>[[Lecture_09|(Previous lecture)]] ... [[Lecture_11|(Next lecture)]]</small> | ||
Latest revision as of 14:51, 10 December 2007
(Previous lecture) ... (Next lecture)
Interpreting Protein Structure
Objectives for this part of the course
- Understand that PDB files contain coordinate information, measured in an orthogonal coordinate system in Å (0.1 nm, 10-10m ).
- Have a sense of the approximate sizes of biological objects.
- Be familiar with the most frequently recurring conformations in protein structure.
- Be aware that these recurring units are just labels and there is some degree of arbitrariness involved in assigning them to real coordinates.
- Understand that more frequently observed conformations are more favourable - for function, for stability or both.
- Be able to superimpose two structures and compare their differences.
- Be able to find structures that are similar to a query.
Links summary
- Backbone Dependent Rotamer Library
- Atlas of Hydrogen Bonds
- Structural Alignment (Wikipedia)
- VAST at the NCBI
- DALI fold classification in Helsinki
- HOMSTRAD at the University of Cambridge
- List of Structural Alignment Software (Wikipedia)
Lecture slides
Analysis of coordinate geometry
Slide 006
Slide 007
Slide 008
Slide 009
Slide 010
Slide 011

Lecture 10, Slide 011
Rotamers are low-energy conformations of side-chain dihedral angles. Only a small number of rotamer states and combinations are significantly populated in natural proteins. This tremendously simplifies protein structure modelling and prediction problems. However it also guides analysis, e.g. in enzyme active sites the rotamers often exist in strained, rare conformations. See the Backbone Dependent Rotamer Library, compiled by Roland Dunbrack.
Rotamers are low-energy conformations of side-chain dihedral angles. Only a small number of rotamer states and combinations are significantly populated in natural proteins. This tremendously simplifies protein structure modelling and prediction problems. However it also guides analysis, e.g. in enzyme active sites the rotamers often exist in strained, rare conformations. See the Backbone Dependent Rotamer Library, compiled by Roland Dunbrack.
Slide 012

Lecture 10, Slide 012
Hydrogen bonds have clear and well defined conformational preferences. The ideal donor-acceptor distance is betwen 2.7 and at most 3.5 Å, the angles between the non-hydrogen donor and acceptor atoms vary only to a small degree. One can view them as mechanisms to "lock-in" parts of protein structure. Cf. the Atlas of Hydrogen Bonds compiled by Ian McDonald and Janet Thornton.
Hydrogen bonds have clear and well defined conformational preferences. The ideal donor-acceptor distance is betwen 2.7 and at most 3.5 Å, the angles between the non-hydrogen donor and acceptor atoms vary only to a small degree. One can view them as mechanisms to "lock-in" parts of protein structure. Cf. the Atlas of Hydrogen Bonds compiled by Ian McDonald and Janet Thornton.
Slide 015
omitted
Slide 016
Slide 017
Slide 018
Slide 019
Slide 020

Lecture 10, Slide 020
An easy way to calculate SAS (solvent accessible surface) areas is to (1) randomly place a given number of points on a sphere around an atom center, (2) erase points that are overlapped by neighboring atoms' spheres and (3) count the number of points that remain. The fraction of remaining points times the surface area of the original sphere approximates the solvent accessible surface area. Surface areas of individual residues are often expressed as relative values, i.e. the actual accessible surface area of a sidechain divided by the area of a maximally solvent-exposed sidechain. This characterizes the degree to which a sidechain is buried or accessible in a protein structure.
An easy way to calculate SAS (solvent accessible surface) areas is to (1) randomly place a given number of points on a sphere around an atom center, (2) erase points that are overlapped by neighboring atoms' spheres and (3) count the number of points that remain. The fraction of remaining points times the surface area of the original sphere approximates the solvent accessible surface area. Surface areas of individual residues are often expressed as relative values, i.e. the actual accessible surface area of a sidechain divided by the area of a maximally solvent-exposed sidechain. This characterizes the degree to which a sidechain is buried or accessible in a protein structure.
Slide 022
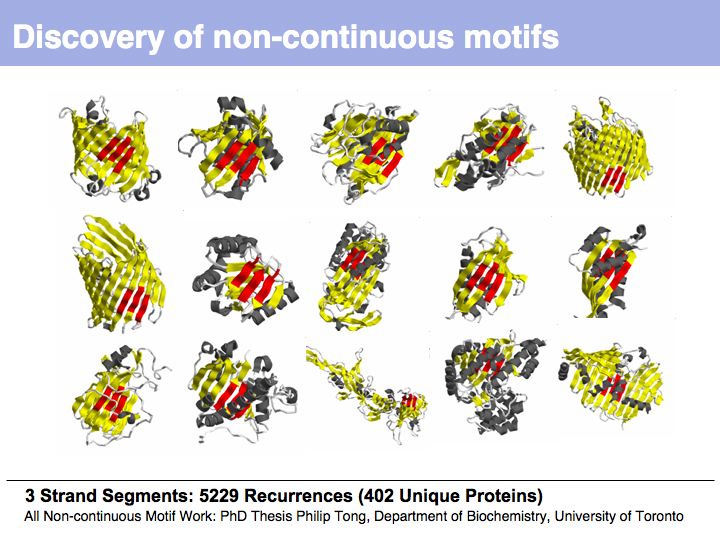
Structure contains recurring units
Slide 024
Slide 031
Slide 032
Slide 033

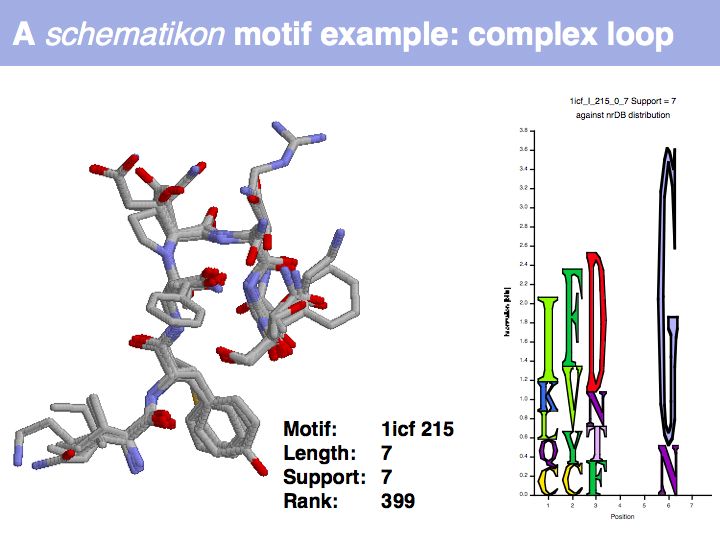
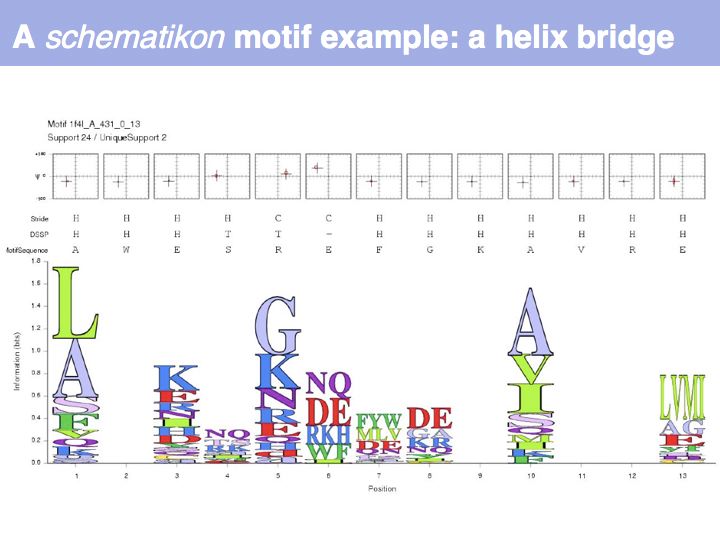
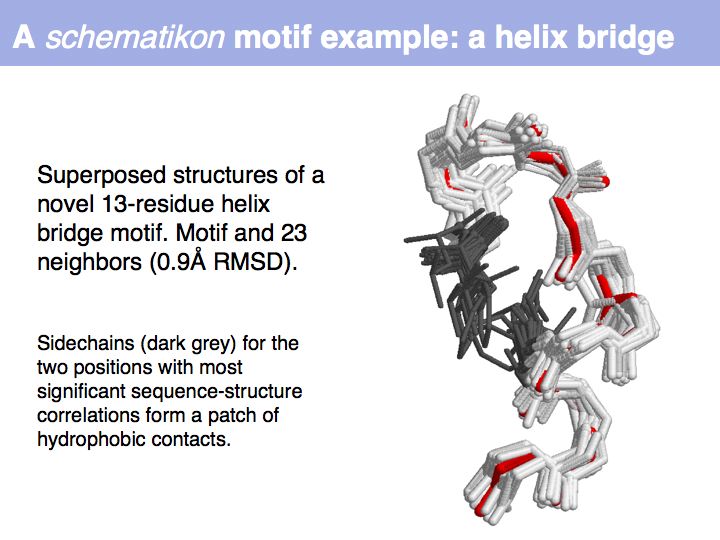
Lecture 10, Slide 033
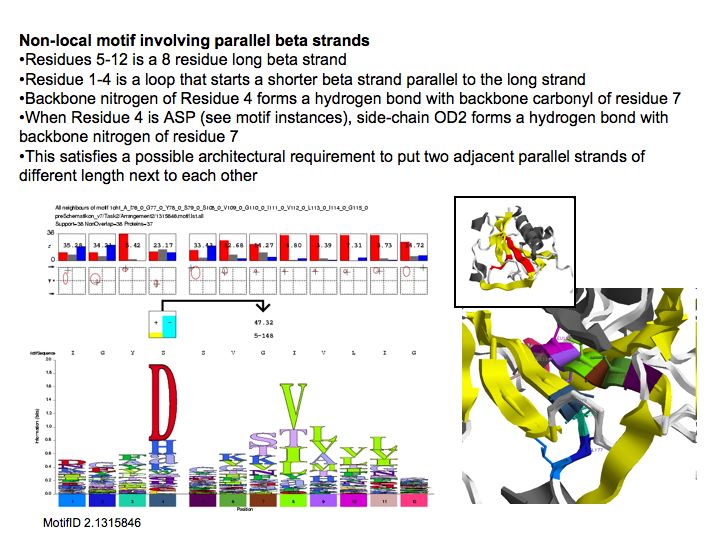
Motifs represent (presumably) low-energy patterns of conformations. They can be discovered in structure datasets by looking for patterns that recur more frequently than expected by random chance. In almost all cases, they have significant statistical propensities to favour particular amino acids in particular positions. This is an example from the schematikon dictionary of recurring structural motifs. he motif is a peptide of length four, recurring seven times. I is ranked in position 444 of all statistiacaly significant motifs. the overlap of backbone atoms is shown in the structural superposition, the propensity for individual amino acids is shown in the sequence logo. Note that the source data consists of non-hmologous protein structures, i.e. the sequence propensities do not represent conservation (since they are not related by common ancestry, but they represent examples of convergent evolution.
Motifs represent (presumably) low-energy patterns of conformations. They can be discovered in structure datasets by looking for patterns that recur more frequently than expected by random chance. In almost all cases, they have significant statistical propensities to favour particular amino acids in particular positions. This is an example from the schematikon dictionary of recurring structural motifs. he motif is a peptide of length four, recurring seven times. I is ranked in position 444 of all statistiacaly significant motifs. the overlap of backbone atoms is shown in the structural superposition, the propensity for individual amino acids is shown in the sequence logo. Note that the source data consists of non-hmologous protein structures, i.e. the sequence propensities do not represent conservation (since they are not related by common ancestry, but they represent examples of convergent evolution.
Slide 034
Slide 035
Slide 036
Slide 037
Slide 038
Slide 039
Slide 040
Slide 041
Propensity predicts stability
Slide 043
Slide 044
Methods: RMSD and superposition
Slide 046

Lecture 10, Slide 046
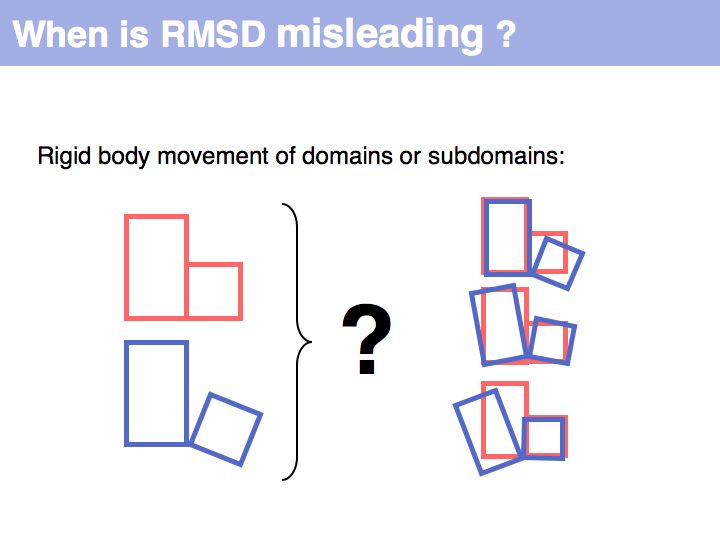
RMSD or root mean square deviation is simply the square root of the average sum of squared coordinate distances. However, this is just a measure of the relationship between two sets of points in space - it depends on the disynace between the point sets, their rotation and the quantitatiy we are interested in: their intrinsic structural similarity. See also: Structural Alignment (Wikipedia)
RMSD or root mean square deviation is simply the square root of the average sum of squared coordinate distances. However, this is just a measure of the relationship between two sets of points in space - it depends on the disynace between the point sets, their rotation and the quantitatiy we are interested in: their intrinsic structural similarity. See also: Structural Alignment (Wikipedia)
Slide 047
Slide 048

Lecture 10, Slide 048
Several pre-superimposed structure sets are available on the Web: VAST at the NCBI DALI fold classification in Helsinki, HOMSTRAD at the University of Cambridge.
Several pre-superimposed structure sets are available on the Web: VAST at the NCBI DALI fold classification in Helsinki, HOMSTRAD at the University of Cambridge.
Slide 049

Lecture 10, Slide 049
List of Structural Alignment Software (Wikipedia)
List of Structural Alignment Software (Wikipedia)
Slide 050
Slide 052
Structural knowledge - mechanistic explanations
Slide 068