Difference between revisions of "Lecture 11"
Jump to navigation
Jump to search
| Line 112: | Line 112: | ||
======Slide 024====== | ======Slide 024====== | ||
[[Image:L11_s024.jpg|frame|none|Lecture 11, Slide 024<br> | [[Image:L11_s024.jpg|frame|none|Lecture 11, Slide 024<br> | ||
| + | Simulated annealing allows a system to be computationally moved out of situations where it is trapped in local minima, and to proceed towards a global minimum on a rough search landscape. | ||
| + | ]] | ||
| − | |||
======Slide 025====== | ======Slide 025====== | ||
[[Image:L11_s025.jpg|frame|none|Lecture 11, Slide 025<br> | [[Image:L11_s025.jpg|frame|none|Lecture 11, Slide 025<br> | ||
Revision as of 06:38, 28 November 2006
(Previous lecture) ... (Next lecture)
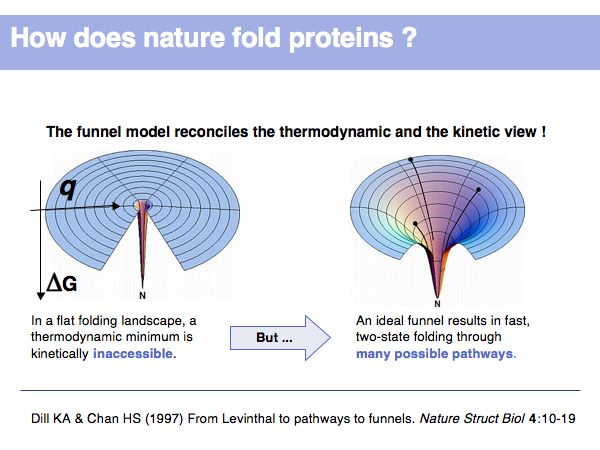
Protein Structure Prediction
...
Add:
- Summary points
- Exercises
- Further reading
Lecture Slides
Slide 001
Lecture 11, Slide 001
Slide 002
Lecture 11, Slide 002
Slide 003
Lecture 11, Slide 003
The observation became famously known as "Levinthal's Paradox", that neither random search nor the postulation of folding pathways can explain how a discrete structure can self-organize, given in a combinatorially large search space. But real proteins do just fine, thank you.
The observation became famously known as "Levinthal's Paradox", that neither random search nor the postulation of folding pathways can explain how a discrete structure can self-organize, given in a combinatorially large search space. But real proteins do just fine, thank you.
Slide 004
Lecture 11, Slide 004
A toy observation on an optimization problem of similar magnitude as the random folding of a protein...
A toy observation on an optimization problem of similar magnitude as the random folding of a protein...
Slide 005
Lecture 11, Slide 005
Slide 006
Lecture 11, Slide 006
Slide 007
Lecture 11, Slide 007
Slide 008
Lecture 11, Slide 008
Slide 009
Lecture 11, Slide 009
Slide 010
Lecture 11, Slide 010
Slide 011
Lecture 11, Slide 011
Slide 012
Lecture 11, Slide 012
Slide 013
Lecture 11, Slide 013
Slide 014
Lecture 11, Slide 014
Slide 015
Lecture 11, Slide 015
Slide 016
Lecture 11, Slide 016
Slide 017
Lecture 11, Slide 017
Slide 018
Lecture 11, Slide 018
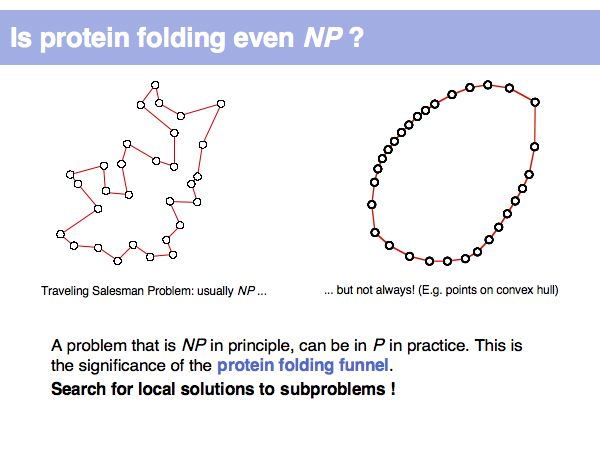
Non-polynomial time-complexity problems are considered intractable, since even as the problem size 'n' grows only modestly, the time requirements grow beyond all bounds and reasonable resources. A 1,000 element problem of O(2n) complexity takes the age of the universe to compute.
Non-polynomial time-complexity problems are considered intractable, since even as the problem size 'n' grows only modestly, the time requirements grow beyond all bounds and reasonable resources. A 1,000 element problem of O(2n) complexity takes the age of the universe to compute.
Slide 019
Lecture 11, Slide 019
Slide 020
Lecture 11, Slide 020
Slide 021
Lecture 11, Slide 021
Slide 022
Lecture 11, Slide 022
Slide 023
Lecture 11, Slide 023
Slide 024
Lecture 11, Slide 024
Simulated annealing allows a system to be computationally moved out of situations where it is trapped in local minima, and to proceed towards a global minimum on a rough search landscape.
Simulated annealing allows a system to be computationally moved out of situations where it is trapped in local minima, and to proceed towards a global minimum on a rough search landscape.
Slide 025
Lecture 11, Slide 025
Slide 026
Lecture 11, Slide 026
Slide 027
Lecture 11, Slide 027
Slide 028
Lecture 11, Slide 028
Slide 029
Lecture 11, Slide 029
Slide 030
Lecture 11, Slide 030
Slide 031
Lecture 11, Slide 031
Slide 032
Lecture 11, Slide 032
Slide 033
Lecture 11, Slide 033
Slide 034
Lecture 11, Slide 034
Slide 035
Lecture 11, Slide 035
Slide 036
Lecture 11, Slide 036
Slide 037
Lecture 11, Slide 037
Slide 038
Lecture 11, Slide 038
