BIO Assignment Week 4

Assignment for Week 4
Domain annotations

Note! This assignment is currently inactive. Major and minor unannounced changes may be made at any time.

Concepts and activities (and reading, if applicable) for this assignment will be topics on next week's quiz.

Introduction

In this assignment we will perform a few computations with coordinate data in PDB files, look more in depth at domain annotations, and compare them across different proteins related to yeast Mbp1. We will write a function in R to help us plot a graphic of the comparison and collaborate to share data for our plots. But first we need to go through a few more R concepts.

Programming R code

First, we will cover essentials of R programming: the fundamental statements that are needed to write programs–conditional expressions and loops, and how to define functions that allow us to use programming code. But let's start with a few more data types of R so we can use the concepts later on: matrices, lists and data frames.

Task:

Please begin by working through the short R - tutorial: matrices section and the following sections on "Lists" and "Data frames".

Note that what we have done here is just the bare minimum on vectors, matrices and lists. The concepts are very generally useful, and there are many useful ways to extract subsets of values. We'll come across these in various parts of R sample code. But unless you read the provided code examples line by line, make sure you understand every single statement and ask if you are not clear about the syntax, this will all be quickly forgotten. Use it or lose it!

R is a full featured programming language and in order to be that, it needs the ability to manipulate Control Flow, i.e. the order in which instructions are executed. By far the most important control flow statement is a conditional branch i.e. the instruction to execute code at alternative points of the program, depending on the presence or absence of a condition. Using such conditional branch instructions, two main types of programming constructs can be realized: conditional expressions and loops.

Conditional expressions

The template for conditional expression in R is:

if( <expression 1> ) {
  <statement 1>
} 
else if ( <expresssion 2> ) {
  <statement 2>
} 
else {
  <statement 3>
}

...where both the else if (...) { ... } and the else (...) block are optional. We have encountered this construct previously, when we assigned the appropriate colors for amino acids in the frequency plot:

if      (names(logRatio[i]) == "F") { barColors[i] <- hydrophobic }
else if (names(logRatio[i]) == "G") { barColors[i] <- plain }
   [... etc ...]
else                                { barColors[i] <- plain }

Logical expressions

We have to consider the <expression> in a bit more detail: anything that is, or produces, or can be interpreted as, a Boolean TRUE or FALSE value can serve as an expression in a conditional statement.

Task:
Here are some examples. Copy the code to an R script, predict what will happen on in each line and try it out:

# A boolean constant is interpreted as is:
if (TRUE)    {print("true")} else {print("false")}
if (FALSE)   {print("true")} else {print("false")}

# Strings of "true" and "false" are coerced to their 
# Boolean equivalent, but contrary to other programming languages
# arbitrary, non-empty or empty strings are not interpreted.
if ("true") {print("true")} else {print("false")}
if ("false") {print("true")} else {print("false")}
if ("widdershins")    {print("true")} else {print("false")}
if ("") {print("true")} else {print("false")}

# All non-zero, defined numbers are TRUE
if (1)      {print("true")} else {print("false")}
if (0)      {print("true")} else {print("false")}
if (-1)     {print("true")} else {print("false")}
if (pi)     {print("true")} else {print("false")}
if (NULL)   {print("true")} else {print("false")}
if (NA)     {print("true")} else {print("false")}
if (NaN)    {print("true")} else {print("false")}
if (Inf)    {print("true")} else {print("false")}

# functions can return Boolean values
affirm <- function() { return(TRUE) }
deny <- function() { return(FALSE) }
if (affirm())    {print("true")} else {print("false")}
if (deny())    {print("true")} else {print("false")}

# N.B. coercion of Booleans into numbers can be done as well
and is sometimes useful: consider ...
a <- c(TRUE, TRUE, FALSE, TRUE, FALSE)
a
as.numeric(a)
sum(a)

# ... or coercing the other way ...
as.logical(-1:1)

Logical operators

To actually write a conditional statement, we have to be able to test a condition and this is what logical operators do. Is something equal to something else? Is it less? Does something exist? Is it a number?

Task:
Here are some examples. Again, predict what will happen ...

TRUE             # Just a statement.

#   unary operator
! TRUE           # NOT ...

# binary operators
FALSE > TRUE     # GREATER THAN ...
FALSE < TRUE     # ... these are coerced to numbers
FALSE < -1        
0 == FALSE       # Careful! == compares, = assigns!!!

"x" == "u"       # using lexical sort order ...
"x" >= "u"
"x" <= "u"
"x" != "u"
"aa" > "u"       # ... not just length, if different.
"abc" < "u"  

TRUE | FALSE    # OR: TRUE if either is true
TRUE & FALSE    # AND: TRUE if both are TRUE

# equality and identity
?identical
a <- c(TRUE)
b <- c(TRUE)
a; b
a == b
identical(a, b)

b <- 1
a; b
a == b
identical(a, b)   # Aha: equal, but not identical


# some other useful tests for conditional expressions
?all
?any
?duplicated
?exists
?is.character
?is.factor
?is.integer
?is.null
?is.numeric
?is.unsorted
?is.vector

Loops

Loops allow you to repeat tasks many times over. The template is:

for (<name> in <vector>) {
   <statement>
}

Task:
Consider the following: Again, copy the code to a script, study it, predict what will happen and then run it.

# simple for loop
for (i in 1:10) {
	print(c(i, i^2, i^3))
}

# Compare excution times: one million square roots from a vector ...
n <- 1000000
x <- 1:n
y <- sqrt(x)

# ... or done explicitly in a for-loop
for (i in 1:n) {
  y[i] <- sqrt (x[i])
}

If you can achieve your result with an R vector expression, it will be faster than using a loop. But sometimes you need to do things explicitly, for example if you need to access intermediate results.

Here is an example to play with loops: a password generator. Passwords are a pain. We need them everywhere, they are frustrating to type, to remember and since the cracking programs are getting smarter they become more and more likely to be broken. Here is a simple password generator that creates random strings with consonant/vowel alterations. These are melodic and easy to memorize, but actually as strong as an 8-character, fully random password that uses all characters of the keyboard such as )He.{2jJ or #h$bB2X^ (which is pretty much unmemorizable). The former is taken from 20⁷ * 7⁷ 10¹⁵ possibilities, the latter is from 94⁸ ~ 6*10¹⁵ possibilities. HIgh-end GPU supported password crackers can test about 10⁹ passwords a second, the passwords generated by this little algorithm would thus take on the order of 10⁶ seconds or eleven days to crack^[1]. This is probably good enough to deter a casual attack.

Task:
Copy, study and run ...

# Suggest memorizable passwords
# Below we use the functions: 
?nchar
?sample
?substr
?paste
?print

#define a string of  consonants ...
con <- "bcdfghjklmnpqrstvwxz"
# ... and a string of of vowels
vow <- "aeiouy"

for (i in 1:10) {  # ten sample passwords to choose from ...
    pass = rep("", 14)  # make an empty character vector
    for (j in 1:7) {  # seven cononant/vbowel pairs to be created ...
        k   <- sample(1:nchar(con), 1) # pick a random index for consonants ...
        ch  <- substr(con,k,k) #  ... get the corresponding character ...
        idx <- (2*j)-1  # ... compute the index where to put the consonant ...
        pass[idx] <- ch # ...  and put it in the right spot

        # same thing for the vowel, but written with less intermediate assignment
        # of results to variables
        k <- sample(1:nchar(vow), 1)
        pass[(2*j)] <- substr(vow,k,k) 
    }
    print( paste(pass, collapse="") )  # collapse the vector in to a string and print
}

Functions

Finally: functions. Functions look very much like the statements we have seen above. the template looks like:

<name> <- function (<parameters>) {
   <statements>
}

The name is any valid name in R. The function is then invoked with name(). The parameter list can be empty, or hold a list of variable names. If variable names are present, you need to enter the corresponding parameters when you execute the function. These assigned variables are then available inside the function to compute with. This is called "passing the variable into the function".

You have encountered a function to choose YFO names. In this function, your Student ID was the parameter. Here is another example to play with: a function that calculates how old you are. In days. This is neat - you can celebrate your 10,000 birthday - or so.

Task:
Copy, explore and run ...

Define the function ...

# A lifedays calculator function

myLifeDays <- function(date = NULL) { # give "date" a default value so we can test whether it has been set
    if (is.null(date)) {
        print ("Enter your birthday as a string in \"YYYY-MM-DD\" format.")
        return()
    }
    x <- strptime(date, "%Y-%m-%d") # convert string to time
    y <- format(Sys.time(), "%Y-%m-%d") # convert "now" to time
    diff <- round(as.numeric(difftime(y, x, unit="days")))
    print(paste("This date was ", diff, " days ago."))
}

Use the function (example)

   myLifeDays("1932-09-25")  # Glenn Gould's birthday

Here is a good opportunity to play and practice programming: modify this function to accept a second argument. When a second argument is present (e.g. 10000) the function should print the calendar date on which the input date will be that number of days ago. Then you could use it to know when to celebrate your 10,000^th lifeDay, or your 777^th anniversary day or whatever.

Enjoy.

Computing with PDB files

Let's apply some of the principles we have covered above to perform computations with biological coordinates.

Task:
First, orient yourself to the actual contents of a PDB file:

Access the PDB page for 1BM8.
Use the pulldown menu towards the top-right to Display files → PDB file.
Study the file, in particular the SEQRES, HELIX and SHEET records, and the structure of ATOM records.

To compute with these coordinates, copy the following R script to your computer and follow it carefully. Make sure you understand each line of code. Ask on the list if anything is not clear.

#bio3d example
# Boris Steipe, October 2013 
setwd("~/Documents/07.TEACHING/36-BCH441\ Bioinformatics\ 2013/")

# In this example of protein structure interpretation, we ...
#   - load the library "bio3D" which supports work with
#     protein structure files,
#   - explore some elementary functions of the library
#   - assemble a script to compare H-bond lengths between
#     alpha-helical and beta-sheet structures.

# bio3d is not available via CRAN, but needs to be installed
# from source. Instructions are here:
# http://thegrantlab.org/bio3d/download/download.html

library(bio3d)

lbio3d() # ... lists the newly installed  functions.
         # they all have help files associated.
         # More information is available on the so-called
         # "vignette", distributed with most R packages:
         # http://thegrantlab.org/bio3d/bio3d_vignette.pdf         

apses <- read.pdb("1bm8")  # load a molecule directly from PDB

# ======== RAMACHANDRAN PLOT ==============================
# Calculate a Ramachandran plot for the structure
tor <- torsion.pdb(apses)
plot(tor$phi, tor$psi)

# As you can see, there are a number of points in the upper-right
# quadrant of the plot. This combination of phi-psi angles defines
# the conformation of a left-handed alpha helix and is generally
# only observed for glycine residues. Let's replot the data, but
# color the points for glycine residues differently. First, we 
# get a vector of glycine residue indices in the structure:

seq <- seq.pdb(apses)

# Explore the result object and extract the indices of GLY resiues.
seq == "G"
which(seq == "G")
as.numeric(which(seq == "G"))
Glys <- as.numeric(which(seq == "G"))

# Now plot all non-gly residues.
# Remember: negative indices exclude items from a vector
plot(tor$phi[-Glys], tor$psi[-Glys], xlim=c(-180,180), ylim=c(-180,180))

# Now plot GLY only, but with red dots:
points(tor$phi[Glys], tor$psi[Glys], pch=21, cex=0.9, bg="#BB0000")

# As you see, four residues in the upper-right quadrant are
# not glycine. But what residues are these? Is there an
# error in our script? 
# You could try as an additional exercise to add the residue
# types or indices of the non-GLY outliers to the plot. 
# Use the function text(). Then you could verify the
# backbone torsion angles in VMD.

# Are there any cis-peptide bonds in the structure?
tor$omega
#... gives us a quick answer. But wait - what values do we
# expect? And why are the values so different?
# Consider this plot: what am I doing here and why?
x <- tor$omega[tor$omega > 0]
x <- c(x, 360 + tor$omega[tor$omega < 0])
hist(x, xlim=c(90,270))
abline(v=180, col="red")

# ======= DISTANCES =================================
# Let's do something a little less trivial and compare
# backbone H-bond distances between helices and strands.
#
# For this, we need to poke around a bit in the way 
# bio3d stores information.
# The basic object is a list:

typeof(apses)

# The list contains components...

names(apses)

# ... which we can access either through the double square
# bracket, or the $ syntax:

apses[["seqres"]]
apses$seqres

# Most of these lists objects can be vectors, other lists
# or scalars

typeof(apses$atom)
typeof(apses$helix)
typeof(apses$sheet)
typeof(apses$seqres)
typeof(apses$xyz)
typeof(apses$calpha)

# This means information can be obtained in several
# different ways. 

# By atom ...
i <- 5
apses$atom[i,]
apses$atom[i, c("x", "y", "z")]   # Note that these are strings!
apses$xyz[c(i*3-2, i*3-1, i*3)]   # Note that these are numbers

# By residue ...
i <- "48"	#string!
apses$atom[apses$atom[,"resno"] == i, ]
i <- 7
apses$seqres[7]

# ... wait, what???
# Isn't that supposed to be the same?
# What's going on here?
# Can you figure it out?

# By chain ...
# (Well - the 1BM8 file has only chain "A", but if there were more
# than one chain, you could select them this way ...). 

paste(aa321(apses$seqres[names(apses$seqres)=="A"]), collapse='')
paste(aa321(apses$atom[apses$atom[,"chain"] == "A" & apses$atom[,"elety"] == "CA","resid"]), collapse='')

# To understand nested statements, especially like the one 
# above, select them piece by piece and execute the pieces to
# see  how the output of one expression works as the argument
# in another expression.



# Back to measuring H-bond distances:
# secondary structure is defined in the list components ...$helix
# and ...$strand.

# We need to 
# - collect all residue indices for alpha helices resp.
#      beta strands;
# - fetch the atom coordinates;
# - calculate all N, O distances using dist.xyz();
# - filter them for distances that indicate H-bonds; and,
# - plot the results.

# Secondary structure can either be obtained from
# definitions contained in many PDB files, or by running
# the DSSP algorithm IF(!) you have it installed on your
# machine. The 1BM8 file contains definitions 

apses$helix
apses$sheet


# (1): collect the residue numbers
# between the segment boundaries.

H <- c() # This will contain the helix residue numbers
for (i in 1:length(apses$helix)) {
	H <- c(H, apses$helix$start[i]:apses$helix$end[i])
}

# Doing the same for the sheet residue numbers requires
# very similar code. Rather than retype the code, it is
# better to write a function that can do both.

getSecondary <- function(sec) {
	R <- c()	
	for (i in 1:length(sec$start)) {
		R <- c(R, sec$start[i]:sec$end[i])
	}
	return(R)
}




# Compare ...
H
getSecondary(apses$helix)

# ... and use for strands

E <- getSecondary(apses$sheet)


# Now here's a problem: these numbers refer to the 
# residue numbers as defined in the atom records. They
# can't be used directly to address e.g. the first, second
# third residue etc. since the first residue has the
# residue number 4...  
apses$atom[1,]

# Therefore we need to
# 1: convert the numbers to strings;
# 2: search for atom records that contain these strings.
#
# Essentially, we don't treat the "residue numbers" as numbers,
# but as generic labels. That's fine, as long as they are unique.

# (2): fetch coordinates of N and O atoms
# for residues in alpha- and beta- conformation.

# For one residue, the procedure goes as follows:

res <- H[17] # pick an arbitrary alpha-helix residue to illustrate
res
res <- as.character(res)
res

# all atom rows for this residue
apses$atom[apses$atom[,"resno"] == res, ]

# add condition: row with "N" atom only
apses$atom[apses$atom[,"resno"] == res & 
           apses$atom[,"elety"] == "N", ]

# add column selection: "x", "y", "z"
apses$atom[apses$atom[,"resno"] == res &
           apses$atom[,"elety"] == "N", 
	       c("x", "y", "z")] 

# convert to numbers
as.numeric (
	apses$atom[apses$atom[,"resno"] == res &
    apses$atom[,"elety"] == "N", 
	c("x", "y", "z")] 
)

# Now we need to add this into a matrix as we iterate over
# the desired residues. We need to execute the procedure
# four times for alpha and beta Ns and Os respectively.
# Rather than duplicate the code four times over,
# we write a function. This is prudent practice for writing
# software: never duplicate code, because if you need to make
# changes it is too easy to forget making the change
# consistently in all copies.


getAtom <- function(PDB, r, AT) {
	# Function to iterate over residue number strings and 
	# return a matrix of x, y, z triplets for each atom
	# of a requested type.
	mat <- c() 	#initialize as empty matrix
	for (i in 1:length(r)) {
		res <- as.character(r[i])	
		v <- as.numeric (
				PDB$atom[PDB$atom[,"resno"] == res &
	    		PDB$atom[,"elety"] == AT, 
				c("x", "y", "z")] 
		)
		mat <- rbind(mat, v)
	}
	return(mat)
}

# Now run the functions with the parameters we need...
H.xyz.N <- getAtom(apses, H, "N")
H.xyz.O <- getAtom(apses, H, "O")
E.xyz.N <- getAtom(apses, E, "N")
E.xyz.O <- getAtom(apses, E, "O")


# (3): calculate distances between N and
# O atoms to find H-bonds.

# We spent most of our effort so far just
# preparing our raw data for analysis. Now
# we can actually start measuring. bio3d provides
# the function dist.xyz() - but we
# could easily code this ourselves.

# Consider the distance of the first (N,O) pair.
H.xyz.N[1,]
H.xyz.O[1,]

a <- H.xyz.N[1,]
b <- H.xyz.O[1,]

dist.xyz(a, b)

# or ...
sqrt( (a[1]-b[1])^2 + (a[2]-b[2])^2 + (a[3]-b[3])^2 )
# ... i.e. pythagoras theorem in 3D.


# Calculating all pairwise distances from a matrix of
# xyz coordinates sounds like a useful function.

PairDist.xyz <- function(a, b) {
	PD <- c()
	for (i in 1:nrow(a)) {
		for (j in 1:nrow(b)) {
			PD <- c(PD, dist.xyz(a[i,], b[j,]))					
		}
	}
	return(PD)
}

# And see what we get:
X <- PairDist.xyz(H.xyz.N, H.xyz.O)
hist(X)

# let's zoom in on the shorter distances, in which we expect
# hydrogen bonds:
hist(X[X < 4.0], breaks=seq(2.0, 4.0, 0.1), xlim=c(2.0,4.0))

# There is a large peak at about 2.2Å, and another
# large peak above 3.5Å. But these are not typical hydrogen
# bond distances! Rather these are (N,O) pairs in peptide
# bonds, and within residues. That's not good, it will
# cause all sorts of problems with statistics later.
# We should exclude all distances between N of a residue
# and O of a preceeding residue, and all (N,O) pairs in the
# same residue. But for this, we need to store atom type
# and residue information with the coordinates. Our code
# will get a bit bulkier. It's often hard to find a good
# balance between terse generic code, and code that
# handles special cases.

# We could do two things:
# - add a column with residue information to the coordinates
# - add a column with atom type information 
# ... but actually we also would need chain information, and
# then we really have almost everything that is contained in the record
# in the first place.

# This suggests a different strategy: let's rewrite our function
# getAtom() to return indices, not coordinates, and use the indices
# to extract coordinates, and THEN we can add all sorts of
# additional constraints.

# Here we set up the function with a default chain argument

getAtomIndex <- function(PDB, V_res, elety, chain="A") {
	# Function to access a bio3d pdb object, iterate over
	# a vector of residues and return a vector of indices
	# to matching atom elements. Nb. bio3d handles insert
	# and alt fields incorrectly: their values should not
	# be NA but " ",  i.e. a single blank. Therefore this
	# function does not test for "alt" and "insert".
	
	v <- c() 	#initialize as empty vector
	for (i in 1:length(V_res)) {
		res <- as.character(V_res[i])	
		x <- which(PDB$atom[,"resno"] == res &
				   PDB$atom[,"chain"] == chain &
	    		   PDB$atom[,"elety"] == elety)
		v <- c(v, x)
	}
	return(v)
}

# test this ...
getAtomIndex(apses, H, "N")
getAtomIndex(apses, H, "O")

# That looks correct: O atoms should be stored three
# rows further down: the sequence of atoms in a PDB
# file is usually N, CA, C, O ... followed by the side
# chain coordinates.

# Now to extract the coordinates and calculate distances.
# Our function needs to take the PDB object and
# two vectors of atom indices as argument, and return
# a vector of pair-distances.

PairDist.idx <- function(PDB, a, b) {
	PD <- c()
	for (i in 1:length(a)) {
		p <- as.numeric(PDB$atom[a[i], c("x", "y", "z")])
		for (j in 1:length(b)) {
			q <- as.numeric(PDB$atom[b[j], c("x", "y", "z")])
			PD <- c(PD, dist.xyz(p, q))					
		}
	}
	return(PD)
}

# Let's see if this looks correct:

H.N <- getAtomIndex(apses, H, "N")
H.O <- getAtomIndex(apses, H, "O")
X <- PairDist.idx(apses, H.N, H.O)
hist(X[X < 4.0], breaks=seq(2.0, 4.0, 0.1), xlim=c(2.0,4.0))

# Now we are back where we started out from, but with 
# a different logic of the function that we can easily
# modify to exclude (N_i, O_i-1) distances (peptide bond),
# and (N_i, O_i) distances (within residue).

HB.idx <- function(PDB, a, b) {
	HBcutoff <- 4.0
	PD <- c()
	for (i in 1:length(a)) {
		p <- as.numeric(PDB$atom[a[i], c("x", "y", "z")])
		res_i <- as.numeric(PDB$atom[a[i], "resno"])
		for (j in 1:length(b)) {
			q <- as.numeric(PDB$atom[b[j], c("x", "y", "z")])
			res_j <- as.numeric(PDB$atom[a[j], "resno"])
			if (res_i != res_j+1 &
			    res_i != res_j     ) {
			    	d <- dist.xyz(p, q)
			    	if (d < HBcutoff) {
 						PD <- c(PD, d)
			    	}
			}
		}
	}
	return(PD)
}

# test this: 
X <- HB.idx(apses, H.N, H.O)
hist(X)

# ... and this looks much more like the distribution we are
# seeking.

# Why did we go along this detour for coding the 
# function? The point is that there are usually
# several ways to use or define datastructures and
# functions. Which one is the best way may not be 
# obvious until you understand the problem better.
# At first, we wrote a very generic function that 
# extracts atom coordinates to be able to compute
# with them. This is simple and elegant. But we
# recognized limitations in that we could not
# make more sophisticated selections that we needed
# to reflect our biological idea of hydrogen
# bonds. Thus we changed our datastructure
# and functions to accomodate our new requirements
# better. You have to be flexible and able to look
# at a task from different angles to succeed.

# Finally we can calculate alpha- and beta- structure
# bonds and compare them. In this section we'll explore
# different options for histogram plots.

H.N <- getAtomIndex(apses, H, "N")
H.O <- getAtomIndex(apses, H, "O")
dH <- HB.idx(apses, H.N, H.O)

E.N <- getAtomIndex(apses, E, "N")
E.O <- getAtomIndex(apses, E, "O")
dE <- HB.idx(apses, E.N, E.O)

# The plain histogram functions without parameters
# give us white stacks.

hist(dH)

# and ... 
hist(dE)

# We can see that the histrograms look different
# but that is better visualized by showing two plots
# in the same window. We use the par() function, for
# more flexible layout, look up the layout() function.
?par
?layout

opar <- par(no.readonly=TRUE)  # store current state
par(mfrow=c(2,1))  # set graphics parameters: 2 rows, one column

# plot two histograms
hist(dH)   
hist(dE)


# add color:
hist(dH, col="#DD0055") 
hist(dE, col="#00AA70")



# For better comparison, plot both in the 
# same window:

hist(dH, col="#DD0055") 
hist(dE, col="#00AA70", add=TRUE)

# ... oops, we dind't reset the graphics parameters.
# You can either close the window, a new window
# will open with default parameters, or ...
par(opar)      # ... reset the graphics parameters

hist(dH, col="#DD0055") 
hist(dE, col="#00AA70", add=TRUE)

# We see that the leftmost column of the sheet bonds
# overlaps the helix bonds. Not good. But we
# can make the colors transparent! We just need to
# add a fourth set of two hexadecimal-numbers to
# the #RRGGBB triplet. Lets use 2/3 transparent,
# in hexadecimal, 1/3 of 256 is x55 - i.e. an
# RGB triplet specied as #RRGGBB55 is only 33%
# opaque:

hist(dH, col="#DD005555") 
hist(dE, col="#00AA7055", add=TRUE)

# To finalize the plots, let's do two more things:
# Explicitly define the breaks, to make sure they
# match up - otherwise they would not need to...
# see for example: 

hist(dH, col="#DD005555") 
hist(dE[dE < 3], col="#00AA7055", add=TRUE)

# Breaks are a parameter in hist() that can
# either be a scaler, to define how many columns
# you want, or a vector, that defines the actual
# breakpoints.
brk=seq(2.4, 4.0, 0.1)

hist(dH, col="#DD005555", breaks=brk) 
hist(dE, col="#00AA7055", breaks=brk, add=TRUE)

# The last thing to do is to think about rescaling the plot.
# You notice that the y-axis is scaled in absolute frequency.
# That gives us some impression of the relative frequency,
# but it is of course skewed by observing relatively more
# or less of one type of secondary structure in a protein.
# As part of the hist() function we can rescale the values so
# that the sum over all is one: set the prameter freq=FALSE.

hist(dH, col="#DD005555", breaks=brk, freq=FALSE) 
hist(dE, col="#00AA7055", breaks=brk, freq=FALSE, add=TRUE)

# Adding labels and legend ...

hH <- hist(dH,
        freq=FALSE,
        breaks=brk, 
		col="#DD005550",
		xlab="(N,O) distance (Å)",
		ylab="Density",
		ylim=c(0,4),
		main="Helix and Sheet H-bond lengths")
hE <- hist(dE,
        freq=FALSE,
        breaks=brk,
        col="#00AA7060",
        add=TRUE)

legend('topright',
		c(paste("alpha (N = ", sum(hH$counts), ")"),
		  paste("beta  (N = ", sum(hE$counts), ")")),
        fill = c("#DD005550", "#00AA7060"), bty = 'n',
        border = NA)
# ===========================================================
# With all the functions we have defined,
# it is easy to try this with a larger protein. In fact
# 3ugj is VERY large. The calculation will take a few
# minutes:

pdb <- read.pdb("3ugj")

H <- getSecondary(pdb$helix)
E <- getSecondary(pdb$sheet)

H.N <- getAtomIndex(pdb, H, "N")
H.O <- getAtomIndex(pdb, H, "O")
dH <- HB.idx(pdb, H.N, H.O)

E.N <- getAtomIndex(pdb, E, "N")
E.O <- getAtomIndex(pdb, E, "O")
dE <- HB.idx(pdb, E.N, E.O)

brk=seq(2.4, 4.0, 0.1)

hH <- hist(dH,
        freq=FALSE,
        breaks=brk, 
		col="#DD005550",
		xlab="(N,O) distance (Å)",
		ylab="Density",
		ylim=c(0,4),
		main="Helix and Sheet H-bond lengths")
hE <- hist(dE,
        freq=FALSE,
        breaks=brk,
        col="#00AA7060",
        add=TRUE)

legend('topright',
		c(paste("alpha (N = ", sum(hH$counts), ")"),
		  paste("beta  (N = ", sum(hE$counts), ")")),
        fill = c("#DD005550", "#00AA7060"), bty = 'n',
        border = NA)

# It looks more and more that the distribution is 
# indeed different. Our sample is large, but derives
# from a single protein.
# To do database scale statistics, we should look 
# at many more proteins. To give you a sense of how,
# let's do this for just ten proteins, taken from
# the architecture level of the CATH database for 
# mixed alpha-beta proteins (see:
# http://www.cathdb.info/browse/browse_hierarchy_tree):

PDBarchitectures <- c("3A4R", "A")
names(PDBarchitectures) <- c("ID", "chain")
PDBarchitectures <- rbind(PDBarchitectures, c("1EWF","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("2VXN","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("1I3K","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("1C0P","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("3QVP","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("1J5U","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("2IMH","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("3NVS","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("1UD9","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("1XKN","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("1OZN","A"))
PDBarchitectures <- rbind(PDBarchitectures, c("2DKJ","A"))

dH <- c()
dE <- c()

for (i in 1:nrow(PDBarchitectures)) {
	pdb <- read.pdb(PDBarchitectures[i,1])
	chain <- PDBarchitectures[i,2]
	H <- getSecondary(pdb$helix)
	H.N <- getAtomIndex(pdb, H, "N", chain)
	H.O <- getAtomIndex(pdb, H, "O", chain)
	dH <- c(dH, HB.idx(pdb, H.N, H.O))
	
	E <- getSecondary(pdb$sheet)
	E.N <- getAtomIndex(pdb, E, "N", chain)
	E.O <- getAtomIndex(pdb, E, "O", chain)
	dE <- c(dE, HB.idx(pdb, E.N, E.O))
}

brk=seq(2.0, 4.0, 0.1)

hH <- hist(dH,
        freq=FALSE,
        breaks=brk, 
		col="#DD005550",
		xlab="(N,O) distance (Å)",
		ylab="Density",
		ylim=c(0,4),
		main="Helix and Sheet H-bond lengths")
hE <- hist(dE,
        freq=FALSE,
        breaks=brk,
        col="#00AA7060",
        add=TRUE)

legend('topright',
		c(paste("alpha (N = ", sum(hH$counts), ")"),
		  paste("beta  (N = ", sum(hE$counts), ")")),
        fill = c("#DD005550", "#00AA7060"), bty = 'n',
        border = NA)

# Nice. 
# That's all.

CDD domain annotation

In the last assignment, you followed a link to CDD Search Results from the RefSeq record for yeast Mbp1 and briefly looked at the information offered by the NCBI's Conserved Domain Database, a database of Position Specific Scoring Matrices that embody domain definitions. Rather than access precomputed results, you can also search CDD with sequences: assuming you have saved the YFO Mbp1 sequence in FASTA format, this is straightforward. If you did not save this sequence, return to Assignment 3 and retrieve it again.

Task:

Access the CDD database at http://www.ncbi.nlm.nih.gov/Structure/cdd/cdd.shtml
Read the information. CDD is a superset of various other database domain annotations as well as NCBI-curated domain definitions.
Copy the YFO Mbp1 FASTA sequence, paste it into the search form and click Submit.
1. On the result page, clik on View full result
2. Note that there are a number of partially overlapping ankyrin domain modules. We will study ankyrin domains in a later assignment.
3. Also note that there may be blocks of sequence colored cyan in the sequence bar. Hover your mouse over the blocks to see what these blocks signify.
4. Open the link to Search for similar domain architecture in a separate window and study it. This is the CDART database. Think about what these results may be useful for.
5. Click on one of the ANK superfamily graphics and see what the associated information looks like: there is a summary of structure and function, links to specific literature and a tree of the relationship of related sequences.

SMART domain annotation

The SMART database at the EMBL in Heidelberg offers an alternative view on domain architectures. I personally find it more useful for annotations because it integrates a number of additional features. You can search by sequence, or by accession number and that raises the question of how to retrieve a database cross-reference from an NCBI sequence identifier to a UniProt sequence ID:

ID mapping

Task:

Access the UniProt ID mapping service at http://www.uniprot.org/mapping/
Paste the RefSeq identifier for YFO Mbp1 into the search field.
Use the menu to choose From RefSeq Protein and To UniprotKB AC–the UniProt Knowledge Base Accession number.
Click on Map to execute the search.
Note the ID - it probably starts with a letter, followed by numbers and letters. Here are some examples for fungal Mbp1-like proteins: P39678 Q5B8H6 Q5ANP5 P41412 etc.
Click on the link, and explore how the UniProt sequence page is similar or different from the RefSeq page.

SMART search

Task:

Access the SMART database at http://smart.embl-heidelberg.de/
Paste the YFO Mbp1 UniProtKB Accession number into the Sequence ID or ACC field.
Check the boxes for:
1. PFAM domains (domains defined by sequence similarity in the PFAM database)
2. signal peptides (using the Gunnar von Heijne's SignalP 4.0 server at the Technical University in Lyngby, Denmark)
3. internal repeats (using the programs ariadne and prospero at the Wellcome Trust Centre for Human Genetics at Oxford University, England)
4. intrinsic protein disorder (using Rune Linding's DisEMBL program at the EMBL in Heidelberg, Germany)
Click on Sequence SMART to run the search and annotation. (In case you get an error like: "Sorry, your entry seems to have no SMART domain ...", let me know and repeat the search with the FASTA sequence instead.)

Study the results. Specifically, have a look at the proteins with similar domain ORGANISATION and COMPOSITION. This is similar to the NCBI's CDART.

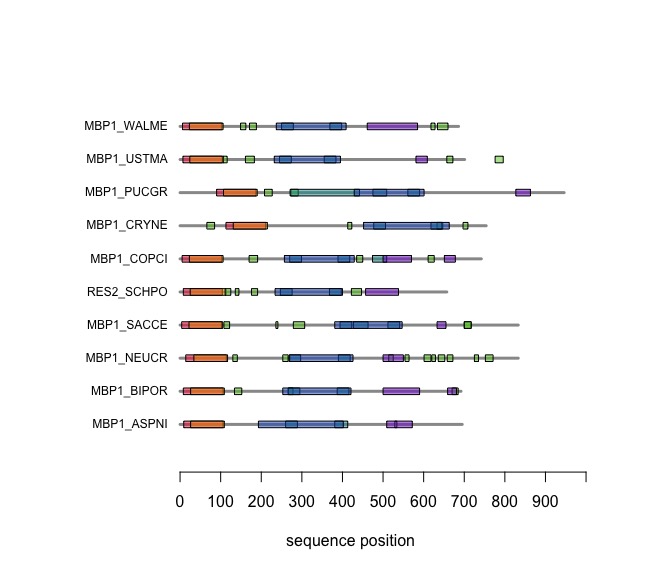
Visual comparison of domain annotations in R

The versatile plotting functions of R allow us to compare domain annotations. I am particularly interested in the distribution of segments that are annotated as being "low-complexity" or "disordered. These are functional features of the amino acid sequence that are often not associated with sequence similarity.

In the following code tutorial, we create a plot similar to the CDD and SMART displays. It is based on the SMART domain annotations of the six-fungal reference species for the course.

Task:
Copy the code to an R script, study and execute it.

# plotDomains
# tutorial and functions to plot a colored rectangle from a list of domain annotations


# First task: create a list structure for the annotations: this is a list of lists
# As you see below, we need to mix strings, numbers and vectors of numbers. In R
# such mixed data types must go into a list.

Mbp1Domains <- list()   # start with an empty list

# For each species annotation, compile the SMART domain annotations in a list.
Mbp1Domains <- rbind(Mbp1Domains, list(  # rbind() appends the list to the existing
    species = "Saccharomyces cerevisiae",
    code    = "SACCE",
    ACC     = "P39678",
    length  = 833,
    KilAN   = c(18,102),       # Note: Vector of (start, end) pairs
    AThook  = NULL,       # Note: NULL, because this annotation was not observed in this sequence
    Seg     = c(108,122,236,241,279,307,700,717),
    DisEMBL = NULL,
    Ankyrin = c(394,423,427,463,512,541),   # Note: Merge overlapping domains, if present
    Coils   = c(633, 655)
    ))

Mbp1Domains <- rbind(Mbp1Domains, list(
    species = "Emericella nidulans",
    code    = "ASPNI",
    ACC     = "Q5B8H6",
    length  = 695,
    KilAN   = c(23,94),
    AThook  = NULL,
    Seg     = c(529,543),
    DisEMBL = NULL,
    Ankyrin = c(260,289,381,413),
    Coils   = c(509,572)
    ))

Mbp1Domains <- rbind(Mbp1Domains, list(
    species = "Candida albicans",
    code    = "CANAL",
    ACC     = "Q5ANP5",
    length  = 852,
    KilAN   = c(19,102),
    AThook  = NULL,
    Seg     = c(351,365,678,692),
    DisEMBL = NULL,
    Ankyrin = c(376,408,412,448,516,545),
    Coils   = c(665,692)
    ))

Mbp1Domains <- rbind(Mbp1Domains, list(
    species = "Neurospora crassa",
    code    = "NEUCR",
    ACC     = "Q7RW59",
    length  = 833,
    KilAN   = c(31,110),
    AThook  = NULL,
    Seg     = c(130,141,253,266,514,525,554,564,601,618,620,629,636,652,658,672,725,735,752,771),
    DisEMBL = NULL,
    Ankyrin = c(268,297,390,419),
    Coils   = c(500,550)
    ))

Mbp1Domains <- rbind(Mbp1Domains, list(
    species = "Schizosaccharomyces pombe",
    code    = "SCHPO",
    ACC     = "P41412",
    length  = 657,
    KilAN   = c(21,97),
    AThook  = NULL,
    Seg     = c(111,125,136,145,176,191,422,447),
    DisEMBL = NULL,
    Ankyrin = c(247,276,368,397),
    Coils   = c(457,538)
    ))

Mbp1Domains <- rbind(Mbp1Domains, list(
    species = "Ustilago maydis",
    code    = "USTMA",
    ACC     = "Q4P117",
    length  = 956,
    KilAN   = c(21,98),
    AThook  = NULL,
    Seg     = c(106,116,161,183,657,672,776,796),
    DisEMBL = NULL,
    Ankyrin = c(245,274,355,384),
    Coils   = c(581,609)
    ))


# Working with data in lists and dataframes can be awkward, since the result
# of filters and slices are themselves lists, not vectors.
# Therefore we need to use the unlist() function a lot. When in doubt: unlist()

#### Boxes #####
# Define a function to draw colored boxes, given input of a vector with
# (start,end) pairs, a color, and the height where the box should go.
drawBoxes <- function(v, c, h) {   # vector of xleft, xright pairs; color; height
    if (is.null(v)) { return() }
    for (i in seq(1,length(v),by=2)) {
        rect(v[i], h-0.1, v[i+1], h+0.1, border="black", col=c)
    }
}

#### Annotations ####
# Define a function to write the species code, draw a grey
# horizontal line and call drawBoxes() for every annotation type
# in the list
drawGene <- function(rIndex) {
    # define colors:
    kil <- "#32344F"
    ank <- "#691A2C"
    seg <- "#598C9E"
    coi <- "#8B9998"
    xxx <- "#EDF7F7"
    
    text (-30, rIndex, adj=1, labels=unlist(Mbp1Domains[rIndex,"code"]), cex=0.75 )
    lines(c(0, unlist(Mbp1Domains[rIndex,"length"])), c(rIndex, rIndex), lwd=3, col="#999999")

    drawBoxes(unlist(Mbp1Domains[rIndex,"KilAN"]),   kil, rIndex)
    drawBoxes(unlist(Mbp1Domains[rIndex,"AThook"]),  xxx, rIndex)
    drawBoxes(unlist(Mbp1Domains[rIndex,"Seg"]),     seg, rIndex)
    drawBoxes(unlist(Mbp1Domains[rIndex,"DisEMBL"]), xxx, rIndex)
    drawBoxes(unlist(Mbp1Domains[rIndex,"Ankyrin"]), ank, rIndex)
    drawBoxes(unlist(Mbp1Domains[rIndex,"Coils"]),   coi, rIndex)
}

#### Plot ####
# define the size of the plot-frame
yMax <- length(Mbp1Domains[,1])   # number of domains in list
xMax <- max(unlist(Mbp1Domains[,"length"]))  # largest sequence length

# plot an empty frame
plot(1,1, xlim=c(-100,xMax), ylim=c(0, yMax) , type="n", yaxt="n", bty="n", xlab="sequence number", ylab="")

# Finally, iterate over all species and call drawGene()
for (i in 1:length(Mbp1Domains[,1])) {
    drawGene(i)
}

# end

When you execute the code, your plot should look similar to this one:

SMART domain annotations for Mbp1 proteins from six fungal species.

Task:

Copy one of the list definitions for Mbp1 domains and edit it with the appropriate values for your own annotations.
Test that you can add the YFO annotation to the plot.
Submit your validated code block to the Student Wiki here. The goal is to compile an overview of all species we are studying in class.
If your working annotation block is in the Wiki before noontime on Wednesday, you will be awarded a 10% bonus on the quiz.

That is all.

Links and resources

Footnotes and references

↑ That's assuming the worst case in that the attacker needs to know the pattern with which the password is formed, i.e. the number of characters and the alphabet that we chose from. But note that there is an even worse case: if the attacker had access to our code and the seed to our random number generator. When the random number generator starts up, a new seed is generated from system time, thus the possible space of seeds can be devastatingly small. But even if a seed is set explicitly with the set.seed() function, that seed is a 32-bit integer and thus can take only a bit more than 4*10⁹ values, six orders of magnitude less than the 10¹⁵ password complexity we thought we had. It turns out that the code may be a much greater vulnerability than the password itself. Keep that in mind. Keep it secret. Keep it safe.

Ask, if things don't work for you!

If anything about the assignment is not clear to you, please ask on the mailing list. You can be certain that others will have had similar problems. Success comes from joining the conversation.

Do consider how to ask your questions so that a meaningful answer is possible:
- How to create a Minimal, Complete, and Verifiable example on stackoverflow and ...
- How to make a great R reproducible example are required reading.

[1] That's assuming the worst case in that the attacker needs to know the pattern with which the password is formed, i.e. the number of characters and the alphabet that we chose from. But note that there is an even worse case: if the attacker had access to our code and the seed to our random number generator. When the random number generator starts up, a new seed is generated from system time, thus the possible space of seeds can be devastatingly small. But even if a seed is set explicitly with the set.seed() function, that seed is a 32-bit integer and thus can take only a bit more than 4*10⁹ values, six orders of magnitude less than the 10¹⁵ password complexity we thought we had. It turns out that the code may be a much greater vulnerability than the password itself. Keep that in mind. Keep it secret. Keep it safe.

[1]

BIO Assignment Week 4

Contents

Introduction

Programming R code

Conditional expressions

Logical expressions

Logical operators

Loops

Functions

Computing with PDB files

CDD domain annotation

SMART domain annotation

ID mapping

SMART search

Visual comparison of domain annotations in R

Links and resources

Footnotes and references

Ask, if things don't work for you!

Navigation menu

Personal tools

Namespaces

Variants

Views

More

Search

Sections

Tools