Difference between revisions of "BIO Assignment Week 4"
m (→Functions) |
|||
| Line 287: | Line 287: | ||
Enjoy. | Enjoy. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== CDD domain annotation == | == CDD domain annotation == | ||
Revision as of 21:15, 4 October 2014
Assignment for Week 4
Domain annotations
Note! This assignment is currently inactive. Major and minor unannounced changes may be made at any time.
Concepts and activities (and reading, if applicable) for this assignment will be topics on next week's quiz.
Contents
Introduction
In this assignment we will perform a few computations with coordinate data in PDB files, look more in depth at domain annotations, and compare them across different proteins related to yeast Mbp1. We will write a function in R to help us plot a graphic of the comparison and collaborate to share data for our plots. But first we need to go through a few more R concepts.
Programming R code
First, we will cover essentials of R programming: the fundamental statements that are needed to write programs–conditional expressions and loops, and how to define functions that allow us to use programming code. But let's start with a few more data types of R so we can use the concepts later on: matrices, lists and data frames.
Task:
Please begin by working through the short R - tutorial: matrices section and the following sections on "Lists" and "Data frames".
Note that what we have done here is just the bare minimum on vectors, matrices and lists. The concepts are very generally useful, and there are many useful ways to extract subsets of values. We'll come across these in various parts of R sample code. But unless you read the provided code examples line by line, make sure you understand every single statement and ask if you are not clear about the syntax, this will all be quickly forgotten. Use it or lose it!
R is a full featured programming language and in order to be that, it needs the ability to manipulate Control Flow, i.e. the order in which instructions are executed. By far the most important control flow statement is a conditional branch i.e. the instruction to execute code at alternative points of the program, depending on the presence or absence of a condition. Using such conditional branch instructions, two main types of programming constructs can be realized: conditional expressions and loops.
Conditional expressions
The template for conditional expression in R is:
if( <expression 1> ) {
<statement 1>
}
else if ( <expresssion 2> ) {
<statement 2>
}
else {
<statement 3>
}...where both the else if (...) { ... } and the else (...) block are optional. We have encountered this construct previously, when we assigned the appropriate colors for amino acids in the frequency plot:
if (names(logRatio[i]) == "F") { barColors[i] <- hydrophobic }
else if (names(logRatio[i]) == "G") { barColors[i] <- plain }
[... etc ...]
else { barColors[i] <- plain }Logical expressions
We have to consider the <expression> in a bit more detail: anything that is, or produces, or can be interpreted as, a Boolean TRUE or FALSE value can serve as an expression in a conditional statement.
Task:
Here are some examples. Copy the code to an R script, predict what will happen on in each line and try it out:
# A boolean constant is interpreted as is:
if (TRUE) {print("true")} else {print("false")}
if (FALSE) {print("true")} else {print("false")}
# Strings of "true" and "false" are coerced to their
# Boolean equivalent, but contrary to other programming languages
# arbitrary, non-empty or empty strings are not interpreted.
if ("true") {print("true")} else {print("false")}
if ("false") {print("true")} else {print("false")}
if ("widdershins") {print("true")} else {print("false")}
if ("") {print("true")} else {print("false")}
# All non-zero, defined numbers are TRUE
if (1) {print("true")} else {print("false")}
if (0) {print("true")} else {print("false")}
if (-1) {print("true")} else {print("false")}
if (pi) {print("true")} else {print("false")}
if (NULL) {print("true")} else {print("false")}
if (NA) {print("true")} else {print("false")}
if (NaN) {print("true")} else {print("false")}
if (Inf) {print("true")} else {print("false")}
# functions can return Boolean values
affirm <- function() { return(TRUE) }
deny <- function() { return(FALSE) }
if (affirm()) {print("true")} else {print("false")}
if (deny()) {print("true")} else {print("false")}
# N.B. coercion of Booleans into numbers can be done as well
and is sometimes useful: consider ...
a <- c(TRUE, TRUE, FALSE, TRUE, FALSE)
a
as.numeric(a)
sum(a)
# ... or coercing the other way ...
as.logical(-1:1)Logical operators
To actually write a conditional statement, we have to be able to test a condition and this is what logical operators do. Is something equal to something else? Is it less? Does something exist? Is it a number?
Task:
Here are some examples. Again, predict what will happen ...
TRUE # Just a statement.
# unary operator
! TRUE # NOT ...
# binary operators
FALSE > TRUE # GREATER THAN ...
FALSE < TRUE # ... these are coerced to numbers
FALSE < -1
0 == FALSE # Careful! == compares, = assigns!!!
"x" == "u" # using lexical sort order ...
"x" >= "u"
"x" <= "u"
"x" != "u"
"aa" > "u" # ... not just length, if different.
"abc" < "u"
TRUE | FALSE # OR: TRUE if either is true
TRUE & FALSE # AND: TRUE if both are TRUE
# equality and identity
?identical
a <- c(TRUE)
b <- c(TRUE)
a; b
a == b
identical(a, b)
b <- 1
a; b
a == b
identical(a, b) # Aha: equal, but not identical
# some other useful tests for conditional expressions
?all
?any
?duplicated
?exists
?is.character
?is.factor
?is.integer
?is.null
?is.numeric
?is.unsorted
?is.vector
Loops
Loops allow you to repeat tasks many times over. The template is:
for (<name> in <vector>) {
<statement>
}Task:
Consider the following: Again, copy the code to a script, study it, predict what will happen and then run it.
# simple for loop
for (i in 1:10) {
print(c(i, i^2, i^3))
}
# Compare excution times: one million square roots from a vector ...
n <- 1000000
x <- 1:n
y <- sqrt(x)
# ... or done explicitly in a for-loop
for (i in 1:n) {
y[i] <- sqrt (x[i])
}If you can achieve your result with an R vector expression, it will be faster than using a loop. But sometimes you need to do things explicitly, for example if you need to access intermediate results.
Here is an example to play with loops: a password generator. Passwords are a pain. We need them everywhere, they are frustrating to type, to remember and since the cracking programs are getting smarter they become more and more likely to be broken. Here is a simple password generator that creates random strings with consonant/vowel alterations. These are melodic and easy to memorize, but actually as strong as an 8-character, fully random password that uses all characters of the keyboard such as )He.{2jJ or #h$bB2X^ (which is pretty much unmemorizable). The former is taken from 207 * 77 1015 possibilities, the latter is from 948 ~ 6*1015 possibilities. HIgh-end GPU supported password crackers can test about 109 passwords a second, the passwords generated by this little algorithm would thus take on the order of 106 seconds or eleven days to crack[1]. This is probably good enough to deter a casual attack.
Task:
Copy, study and run ...
# Suggest memorizable passwords
# Below we use the functions:
?nchar
?sample
?substr
?paste
?print
#define a string of consonants ...
con <- "bcdfghjklmnpqrstvwxz"
# ... and a string of of vowels
vow <- "aeiouy"
for (i in 1:10) { # ten sample passwords to choose from ...
pass = rep("", 14) # make an empty character vector
for (j in 1:7) { # seven consonant/vowel pairs to be created ...
k <- sample(1:nchar(con), 1) # pick a random index for consonants ...
ch <- substr(con,k,k) # ... get the corresponding character ...
idx <- (2*j)-1 # ... compute the position (index) of where to put the consonant ...
pass[idx] <- ch # ... and put it in the right spot
# same thing for the vowel, but coded with fewer intermediate assignments
# of results to variables
k <- sample(1:nchar(vow), 1)
pass[(2*j)] <- substr(vow,k,k)
}
print( paste(pass, collapse="") ) # collapse the vector in to a string and print
}Functions
Finally: functions. Functions look very much like the statements we have seen above. the template looks like:
<name> <- function (<parameters>) {
<statements>
}In this statement, the function is assigned to the name - any valid name in R. Once it is assigned, it the function can be invoked with name(). The parameter list (the values we write into the parentheses followin the function name) can be empty, or hold a list of variable names. If variable names are present, you need to enter the corresponding parameters when you execute the function. These assigned variables are available inside the function, and can be used for computations. This is called "passing the variable into the function".
You have encountered a function to choose YFO names. In this function, your Student ID was the parameter. Here is another example to play with: a function that calculates how old you are. In days. This is neat - you can celebrate your 10,000 birthday - or so.
Task:
Copy, explore and run ...
- Define the function ...
# A lifedays calculator function
myLifeDays <- function(date = NULL) { # give "date" a default value so we can test whether it has been set
if (is.null(date)) {
print ("Enter your birthday as a string in \"YYYY-MM-DD\" format.")
return()
}
x <- strptime(date, "%Y-%m-%d") # convert string to time
y <- format(Sys.time(), "%Y-%m-%d") # convert "now" to time
diff <- round(as.numeric(difftime(y, x, unit="days")))
print(paste("This date was ", diff, " days ago."))
}- Use the function (example)
myLifeDays("1932-09-25") # Glenn Gould's birthdayHere is a good opportunity to play and practice programming: modify this function to accept a second argument. When a second argument is present (e.g. 10000) the function should print the calendar date on which the input date will be that number of days ago. Then you could use it to know when to celebrate your 10,000th lifeDay, or your 777th anniversary day or whatever.
Enjoy.
CDD domain annotation
In the last assignment, you followed a link to CDD Search Results from the RefSeq record for yeast Mbp1 and briefly looked at the information offered by the NCBI's Conserved Domain Database, a database of Position Specific Scoring Matrices that embody domain definitions. Rather than access precomputed results, you can also search CDD with sequences: assuming you have saved the YFO Mbp1 sequence in FASTA format, this is straightforward. If you did not save this sequence, return to Assignment 3 and retrieve it again.
Task:
- Access the CDD database at http://www.ncbi.nlm.nih.gov/Structure/cdd/cdd.shtml
- Read the information. CDD is a superset of various other database domain annotations as well as NCBI-curated domain definitions.
- Copy the YFO Mbp1 FASTA sequence, paste it into the search form and click Submit.
- On the result page, clik on View full result
- Note that there are a number of partially overlapping ankyrin domain modules. We will study ankyrin domains in a later assignment.
- Also note that there may be blocks of sequence colored cyan in the sequence bar. Hover your mouse over the blocks to see what these blocks signify.
- Open the link to Search for similar domain architecture in a separate window and study it. This is the CDART database. Think about what these results may be useful for.
- Click on one of the ANK superfamily graphics and see what the associated information looks like: there is a summary of structure and function, links to specific literature and a tree of the relationship of related sequences.
SMART domain annotation
The SMART database at the EMBL in Heidelberg offers an alternative view on domain architectures. I personally find it more useful for annotations because it integrates a number of additional features. You can search by sequence, or by accession number and that raises the question of how to retrieve a database cross-reference from an NCBI sequence identifier to a UniProt sequence ID:
ID mapping
Task:
- Access the UniProt ID mapping service at http://www.uniprot.org/mapping/
- Paste the RefSeq identifier for YFO Mbp1 into the search field.
- Use the menu to choose From RefSeq Protein and To UniprotKB AC–the UniProt Knowledge Base Accession number.
- Click on Map to execute the search.
- Note the ID - it probably starts with a letter, followed by numbers and letters. Here are some examples for fungal Mbp1-like proteins:
P39678 Q5B8H6 Q5ANP5 P41412etc. - Click on the link, and explore how the UniProt sequence page is similar or different from the RefSeq page.
SMART search
Task:
- Access the SMART database at http://smart.embl-heidelberg.de/
- Paste the YFO Mbp1 UniProtKB Accession number into the Sequence ID or ACC field.
- Check the boxes for:
- PFAM domains (domains defined by sequence similarity in the PFAM database)
- signal peptides (using the Gunnar von Heijne's SignalP 4.0 server at the Technical University in Lyngby, Denmark)
- internal repeats (using the programs ariadne and prospero at the Wellcome Trust Centre for Human Genetics at Oxford University, England)
- intrinsic protein disorder (using Rune Linding's DisEMBL program at the EMBL in Heidelberg, Germany)
- Click on Sequence SMART to run the search and annotation. (In case you get an error like: "Sorry, your entry seems to have no SMART domain ...", let me know and repeat the search with the FASTA sequence instead.)
Study the results. Specifically, have a look at the proteins with similar domain ORGANISATION and COMPOSITION. This is similar to the NCBI's CDART.
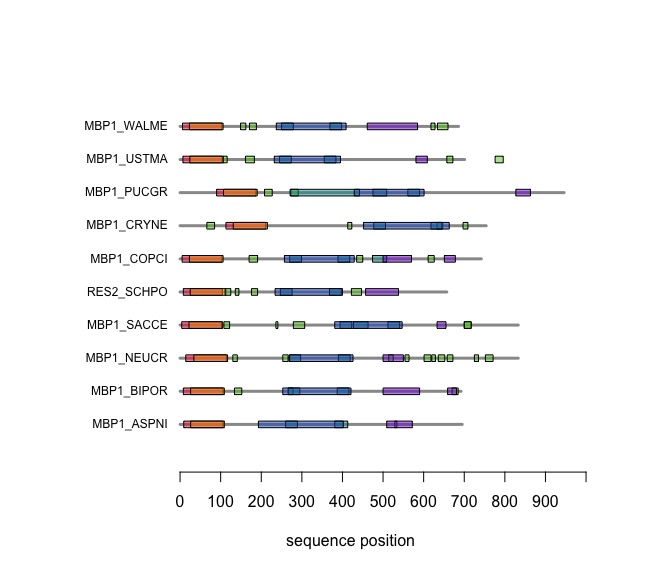
Visual comparison of domain annotations in R
The versatile plotting functions of R allow us to compare domain annotations. I am particularly interested in the distribution of segments that are annotated as being "low-complexity" or "disordered. These are functional features of the amino acid sequence that are often not associated with sequence similarity.
In the following code tutorial, we create a plot similar to the CDD and SMART displays. It is based on the SMART domain annotations of the six-fungal reference species for the course.
Task:
Copy the code to an R script, study and execute it.
# plotDomains
# tutorial and functions to plot a colored rectangle from a list of domain annotations
# First task: create a list structure for the annotations: this is a list of lists
# As you see below, we need to mix strings, numbers and vectors of numbers. In R
# such mixed data types must go into a list.
Mbp1Domains <- list() # start with an empty list
# For each species annotation, compile the SMART domain annotations in a list.
Mbp1Domains <- rbind(Mbp1Domains, list( # rbind() appends the list to the existing
species = "Saccharomyces cerevisiae",
code = "SACCE",
ACC = "P39678",
length = 833,
KilAN = c(18,102), # Note: Vector of (start, end) pairs
AThook = NULL, # Note: NULL, because this annotation was not observed in this sequence
Seg = c(108,122,236,241,279,307,700,717),
DisEMBL = NULL,
Ankyrin = c(394,423,427,463,512,541), # Note: Merge overlapping domains, if present
Coils = c(633, 655)
))
Mbp1Domains <- rbind(Mbp1Domains, list(
species = "Emericella nidulans",
code = "ASPNI",
ACC = "Q5B8H6",
length = 695,
KilAN = c(23,94),
AThook = NULL,
Seg = c(529,543),
DisEMBL = NULL,
Ankyrin = c(260,289,381,413),
Coils = c(509,572)
))
Mbp1Domains <- rbind(Mbp1Domains, list(
species = "Candida albicans",
code = "CANAL",
ACC = "Q5ANP5",
length = 852,
KilAN = c(19,102),
AThook = NULL,
Seg = c(351,365,678,692),
DisEMBL = NULL,
Ankyrin = c(376,408,412,448,516,545),
Coils = c(665,692)
))
Mbp1Domains <- rbind(Mbp1Domains, list(
species = "Neurospora crassa",
code = "NEUCR",
ACC = "Q7RW59",
length = 833,
KilAN = c(31,110),
AThook = NULL,
Seg = c(130,141,253,266,514,525,554,564,601,618,620,629,636,652,658,672,725,735,752,771),
DisEMBL = NULL,
Ankyrin = c(268,297,390,419),
Coils = c(500,550)
))
Mbp1Domains <- rbind(Mbp1Domains, list(
species = "Schizosaccharomyces pombe",
code = "SCHPO",
ACC = "P41412",
length = 657,
KilAN = c(21,97),
AThook = NULL,
Seg = c(111,125,136,145,176,191,422,447),
DisEMBL = NULL,
Ankyrin = c(247,276,368,397),
Coils = c(457,538)
))
Mbp1Domains <- rbind(Mbp1Domains, list(
species = "Ustilago maydis",
code = "USTMA",
ACC = "Q4P117",
length = 956,
KilAN = c(21,98),
AThook = NULL,
Seg = c(106,116,161,183,657,672,776,796),
DisEMBL = NULL,
Ankyrin = c(245,274,355,384),
Coils = c(581,609)
))
# Working with data in lists and dataframes can be awkward, since the result
# of filters and slices are themselves lists, not vectors.
# Therefore we need to use the unlist() function a lot. When in doubt: unlist()
#### Boxes #####
# Define a function to draw colored boxes, given input of a vector with
# (start,end) pairs, a color, and the height where the box should go.
drawBoxes <- function(v, c, h) { # vector of xleft, xright pairs; color; height
if (is.null(v)) { return() }
for (i in seq(1,length(v),by=2)) {
rect(v[i], h-0.1, v[i+1], h+0.1, border="black", col=c)
}
}
#### Annotations ####
# Define a function to write the species code, draw a grey
# horizontal line and call drawBoxes() for every annotation type
# in the list
drawGene <- function(rIndex) {
# define colors:
kil <- "#32344F"
ank <- "#691A2C"
seg <- "#598C9E"
coi <- "#8B9998"
xxx <- "#EDF7F7"
text (-30, rIndex, adj=1, labels=unlist(Mbp1Domains[rIndex,"code"]), cex=0.75 )
lines(c(0, unlist(Mbp1Domains[rIndex,"length"])), c(rIndex, rIndex), lwd=3, col="#999999")
drawBoxes(unlist(Mbp1Domains[rIndex,"KilAN"]), kil, rIndex)
drawBoxes(unlist(Mbp1Domains[rIndex,"AThook"]), xxx, rIndex)
drawBoxes(unlist(Mbp1Domains[rIndex,"Seg"]), seg, rIndex)
drawBoxes(unlist(Mbp1Domains[rIndex,"DisEMBL"]), xxx, rIndex)
drawBoxes(unlist(Mbp1Domains[rIndex,"Ankyrin"]), ank, rIndex)
drawBoxes(unlist(Mbp1Domains[rIndex,"Coils"]), coi, rIndex)
}
#### Plot ####
# define the size of the plot-frame
yMax <- length(Mbp1Domains[,1]) # number of domains in list
xMax <- max(unlist(Mbp1Domains[,"length"])) # largest sequence length
# plot an empty frame
plot(1,1, xlim=c(-100,xMax), ylim=c(0, yMax) , type="n", yaxt="n", bty="n", xlab="sequence number", ylab="")
# Finally, iterate over all species and call drawGene()
for (i in 1:length(Mbp1Domains[,1])) {
drawGene(i)
}
# end
When you execute the code, your plot should look similar to this one:
Task:
- Copy one of the list definitions for Mbp1 domains and edit it with the appropriate values for your own annotations.
- Test that you can add the YFO annotation to the plot.
- Submit your validated code block to the Student Wiki here. The goal is to compile an overview of all species we are studying in class.
- If your working annotation block is in the Wiki before noontime on Wednesday, you will be awarded a 10% bonus on the quiz.
- That is all.
Links and resources
Footnotes and references
- ↑ That's assuming the worst case in that the attacker needs to know the pattern with which the password is formed, i.e. the number of characters and the alphabet that we chose from. But note that there is an even worse case: if the attacker had access to our code and the seed to our random number generator. When the random number generator starts up, a new seed is generated from system time, thus the possible space of seeds can be devastatingly small. But even if a seed is set explicitly with the
set.seed()function, that seed is a 32-bit integer and thus can take only a bit more than 4*109 values, six orders of magnitude less than the 1015 password complexity we thought we had. It turns out that the code may be a much greater vulnerability than the password itself. Keep that in mind. Keep it secret. Keep it safe.
Ask, if things don't work for you!
- If anything about the assignment is not clear to you, please ask on the mailing list. You can be certain that others will have had similar problems. Success comes from joining the conversation.
- Do consider how to ask your questions so that a meaningful answer is possible:
- How to create a Minimal, Complete, and Verifiable example on stackoverflow and ...
- How to make a great R reproducible example are required reading.